题目
已知(x)=dfrac (|x|)(x),则f(x)在x=0处( )不连续但可导可导连续但不可导极限不存在
已知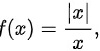 则f(x)在x=0处( )
则f(x)在x=0处( )
- 不连续但可导
- 可导
- 连续但不可导
- 极限不存在
题目解答
答案
本题答案选D
因为分母中含有x,所以x=0处函数是没有意义的
因为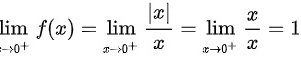
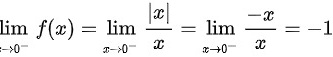
x=0处的左右极限是不相等的,所以函数在x=0处是不连续的,函数在x=0处极限是不存在的,因此函数也是不可导的
因此选项A,B,C错误
D正确
解析
步骤 1:定义函数$f(x)$
函数$f(x)=\dfrac {|x|}{x}$,其中$|x|$表示$x$的绝对值。当$x>0$时,$|x|=x$;当$x<0$时,$|x|=-x$。因此,$f(x)$可以写为:
$$
f(x) = \begin{cases}
1, & x > 0 \\
-1, & x < 0
\end{cases}
$$
步骤 2:检查函数在$x=0$处的定义
由于$f(x)$的定义中分母为$x$,当$x=0$时,函数$f(x)$没有定义,即$f(0)$不存在。
步骤 3:计算$x=0$处的左右极限
- 当$x$从右侧(正数)趋近于$0$时,$f(x)=1$,因此$\lim _{x\rightarrow {0}^{+}}f(x)=1$。
- 当$x$从左侧(负数)趋近于$0$时,$f(x)=-1$,因此$\lim _{x\rightarrow {0}^{-}}f(x)=-1$。
步骤 4:判断函数在$x=0$处的连续性和可导性
由于$\lim _{x\rightarrow {0}^{+}}f(x)\neq \lim _{x\rightarrow {0}^{-}}f(x)$,即左右极限不相等,所以函数在$x=0$处不连续。由于函数在$x=0$处不连续,因此函数在$x=0$处也不可导。
函数$f(x)=\dfrac {|x|}{x}$,其中$|x|$表示$x$的绝对值。当$x>0$时,$|x|=x$;当$x<0$时,$|x|=-x$。因此,$f(x)$可以写为:
$$
f(x) = \begin{cases}
1, & x > 0 \\
-1, & x < 0
\end{cases}
$$
步骤 2:检查函数在$x=0$处的定义
由于$f(x)$的定义中分母为$x$,当$x=0$时,函数$f(x)$没有定义,即$f(0)$不存在。
步骤 3:计算$x=0$处的左右极限
- 当$x$从右侧(正数)趋近于$0$时,$f(x)=1$,因此$\lim _{x\rightarrow {0}^{+}}f(x)=1$。
- 当$x$从左侧(负数)趋近于$0$时,$f(x)=-1$,因此$\lim _{x\rightarrow {0}^{-}}f(x)=-1$。
步骤 4:判断函数在$x=0$处的连续性和可导性
由于$\lim _{x\rightarrow {0}^{+}}f(x)\neq \lim _{x\rightarrow {0}^{-}}f(x)$,即左右极限不相等,所以函数在$x=0$处不连续。由于函数在$x=0$处不连续,因此函数在$x=0$处也不可导。