题目
求limn[ln(n+2)-ln n]=______。
求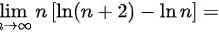 ______。
______。
题目解答
答案
因为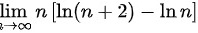
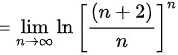
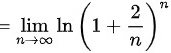
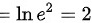 ,
,
所以正确答案为2。
解析
考查要点:本题主要考查自然对数的运算性质、等价无穷小替换以及重要极限公式的应用。
解题核心思路:
将对数的差转化为对数的商,利用$\ln a - \ln b = \ln \frac{a}{b}$简化表达式,再结合等价无穷小替换或重要极限公式求解。
破题关键点:
- 变形表达式:将$\ln(n+2) - \ln n$转化为$\ln\left(1+\frac{2}{n}\right)$。
- 应用等价无穷小:当$n \to \infty$时,$\ln\left(1+\frac{2}{n}\right) \sim \frac{2}{n}$。
- 结合重要极限:利用$\lim_{n \to \infty} \left(1+\frac{a}{n}\right)^n = e^a$,将原式转化为对数形式求解。
步骤1:变形表达式
原式可变形为:
$n \left[ \ln(n+2) - \ln n \right] = n \cdot \ln\left( \frac{n+2}{n} \right) = n \cdot \ln\left(1 + \frac{2}{n}\right).$
步骤2:应用等价无穷小替换
当$n \to \infty$时,$\frac{2}{n} \to 0$,根据等价无穷小$\ln(1+x) \sim x$(当$x \to 0$时),有:
$\ln\left(1 + \frac{2}{n}\right) \sim \frac{2}{n}.$
步骤3:代入并化简
将等价无穷小代入原式:
$n \cdot \frac{2}{n} = 2.$
步骤4(备选方法):利用重要极限公式
将原式写成对数形式:
$n \cdot \ln\left(1 + \frac{2}{n}\right) = \ln\left( \left(1 + \frac{2}{n}\right)^n \right).$
当$n \to \infty$时,$\left(1 + \frac{2}{n}\right)^n \to e^2$,因此:
$\ln\left( e^2 \right) = 2.$