题目
12.设方程 +sqrt ({x)^2+(y)^2+(z)^2}=sqrt (2) 确定了函数 =z(x,y), 则z(x,y)-|||-在点 (1,0,-1) 处的全微分 =[ ] .-|||-(A) +sqrt (2)dy (B) -dx+sqrt (2)dy-|||-(C) -dx-sqrt (2)dy (D) -sqrt (2)dy
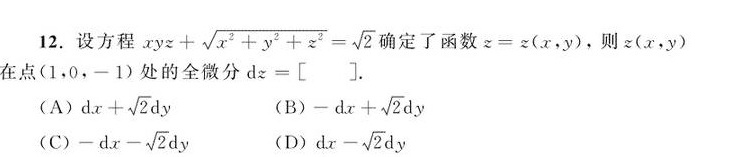
题目解答
答案

解析
步骤 1:对给定方程求偏导数
给定方程为 $xyz+\sqrt {{x}^{2}+{y}^{2}+{z}^{2}}=\sqrt {2}$。为了找到函数 $z=z(x,y)$ 在点 $(1,0,-1)$ 处的全微分 $dz$,我们首先需要对方程两边对 $x$ 和 $y$ 求偏导数。
步骤 2:求偏导数 $z_x$ 和 $z_y$
对 $x$ 求偏导数,得到 $yz+xyz_x+\dfrac {x+z{z}_{x}}{\sqrt {{x}^{2}+{y}^{2}+{z}^{2}}}=0$。将 $x=1$,$y=0$,$z=-1$ 代入上式,得 $z_x=1$。
对 $y$ 求偏导数,得到 $xz+xyz_y+\dfrac {y+z{z}_{y}}{\sqrt {{x}^{2}+{y}^{2}+{z}^{2}}}=0$。将 $x=1$,$y=0$,$z=-1$ 代入上式,得 $z_y=-\sqrt{2}$。
步骤 3:计算全微分 $dz$
根据全微分公式 $dz=z_xdx+z_ydy$,将 $z_x=1$ 和 $z_y=-\sqrt{2}$ 代入,得到 $dz=dx-\sqrt{2}dy$。
给定方程为 $xyz+\sqrt {{x}^{2}+{y}^{2}+{z}^{2}}=\sqrt {2}$。为了找到函数 $z=z(x,y)$ 在点 $(1,0,-1)$ 处的全微分 $dz$,我们首先需要对方程两边对 $x$ 和 $y$ 求偏导数。
步骤 2:求偏导数 $z_x$ 和 $z_y$
对 $x$ 求偏导数,得到 $yz+xyz_x+\dfrac {x+z{z}_{x}}{\sqrt {{x}^{2}+{y}^{2}+{z}^{2}}}=0$。将 $x=1$,$y=0$,$z=-1$ 代入上式,得 $z_x=1$。
对 $y$ 求偏导数,得到 $xz+xyz_y+\dfrac {y+z{z}_{y}}{\sqrt {{x}^{2}+{y}^{2}+{z}^{2}}}=0$。将 $x=1$,$y=0$,$z=-1$ 代入上式,得 $z_y=-\sqrt{2}$。
步骤 3:计算全微分 $dz$
根据全微分公式 $dz=z_xdx+z_ydy$,将 $z_x=1$ 和 $z_y=-\sqrt{2}$ 代入,得到 $dz=dx-\sqrt{2}dy$。