题目
设→(a)→∞-|||-lim _(narrow infty )(x)_(n)=+infty lim _(narrow infty )(y)_(n)=infty lim _(narrow infty )(n)_(n)=A 则下列命题中正确的是( ). →(a)→∞-|||-lim _(narrow infty )(x)_(n)=+infty lim _(narrow infty )(y)_(n)=infty lim _(narrow infty )(n)_(n)=A→(a)→∞-|||-lim _(narrow infty )(x)_(n)=+infty lim _(narrow infty )(y)_(n)=infty lim _(narrow infty )(n)_(n)=A→(a)→∞-|||-lim _(narrow infty )(x)_(n)=+infty lim _(narrow infty )(y)_(n)=infty lim _(narrow infty )(n)_(n)=A→(a)→∞-|||-lim _(narrow infty )(x)_(n)=+infty lim _(narrow infty )(y)_(n)=infty lim _(narrow infty )(n)_(n)=A
设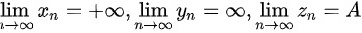 则下列命题中正确的是( ).
则下列命题中正确的是( ).
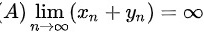
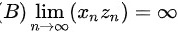
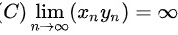
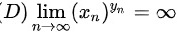
题目解答
答案
设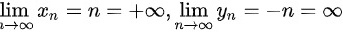 ,
,
则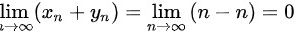 ,
,
所以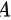 选项错误.
选项错误.
设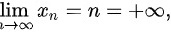
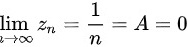 ,
,
则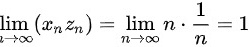 ,
,
所以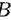 选项错误.
选项错误.
由极限定义可知,
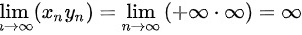 ,
,
所以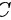 选项正确.
选项正确.
设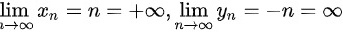 ,则
,则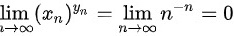 ,
,
所以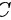 选项错误.
选项错误.
综上所述,答案为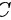 .
.
解析
步骤 1:分析选项A
设$\lim _{n\rightarrow \infty }{x}_{n}=+\infty $ $\lim _{n\rightarrow \infty }{y}_{n}=-n=\infty $ n→∞,
则$\lim _{n\rightarrow \infty }({x}_{n}+{y}_{n})=\lim _{n\rightarrow \infty }(n-n)=0$,
所以选项A错误.
步骤 2:分析选项B
设$\lim _{x\rightarrow 1}\dfrac {1}{2}$,$\lim _{n\rightarrow \infty }{z}_{n}=\dfrac {1}{n}=A=0$,
则$\lim _{n\rightarrow \infty }({x}_{n}{z}_{n})=\lim _{n\rightarrow \infty }n\cdot \dfrac {1}{n}=1$,
所以选项B错误.
步骤 3:分析选项C
由极限定义可知,
$\lim _{n\rightarrow \infty }({x}_{n}{y}_{n})=\lim _{n\rightarrow \infty }(+\infty \cdot \infty )=\infty $,
所以选项C正确.
步骤 4:分析选项D
设$\lim _{n\rightarrow \infty }{x}_{n}=+\infty $ $\lim _{n\rightarrow \infty }{y}_{n}=-n=\infty $ n→∞,则$\lim _{n\rightarrow \infty }{({x}_{n})}^{{y}_{n}}=\lim _{n\rightarrow \infty }{n}^{-n}=0$,
所以选项D错误.
设$\lim _{n\rightarrow \infty }{x}_{n}=+\infty $ $\lim _{n\rightarrow \infty }{y}_{n}=-n=\infty $ n→∞,
则$\lim _{n\rightarrow \infty }({x}_{n}+{y}_{n})=\lim _{n\rightarrow \infty }(n-n)=0$,
所以选项A错误.
步骤 2:分析选项B
设$\lim _{x\rightarrow 1}\dfrac {1}{2}$,$\lim _{n\rightarrow \infty }{z}_{n}=\dfrac {1}{n}=A=0$,
则$\lim _{n\rightarrow \infty }({x}_{n}{z}_{n})=\lim _{n\rightarrow \infty }n\cdot \dfrac {1}{n}=1$,
所以选项B错误.
步骤 3:分析选项C
由极限定义可知,
$\lim _{n\rightarrow \infty }({x}_{n}{y}_{n})=\lim _{n\rightarrow \infty }(+\infty \cdot \infty )=\infty $,
所以选项C正确.
步骤 4:分析选项D
设$\lim _{n\rightarrow \infty }{x}_{n}=+\infty $ $\lim _{n\rightarrow \infty }{y}_{n}=-n=\infty $ n→∞,则$\lim _{n\rightarrow \infty }{({x}_{n})}^{{y}_{n}}=\lim _{n\rightarrow \infty }{n}^{-n}=0$,
所以选项D错误.