题目
3、(2007年)已知当x→0时, ^2ln (1+(x)^2) 是sin"x的高阶无穷小,而sin"x又是 https:/img.zuoyebang.cc/zyb_0b0069c24a40acb66d83ed049349c046.jpg-cos x-|||-的高阶无穷小,则正整数 n= ()-|||-A、1 B、2 C、3 D、4
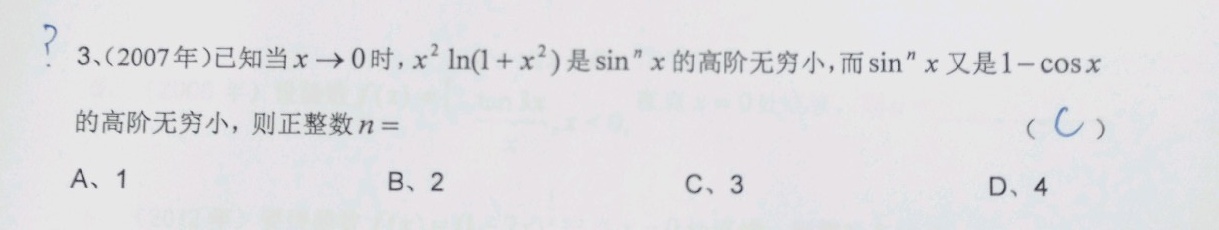
题目解答
答案

解析
步骤 1:确定 ${x}^{2}\ln (1+{x}^{2})$ 的等价无穷小
当 $x \to 0$ 时,$\ln(1+x^2)$ 可以用泰勒展开式近似为 $x^2$,因此 ${x}^{2}\ln (1+{x}^{2})$ 等价于 $x^4$。
步骤 2:确定 $1-\cos x$ 的等价无穷小
当 $x \to 0$ 时,$1-\cos x$ 可以用泰勒展开式近似为 $\frac{x^2}{2}$。
步骤 3:确定 $\sin^nx$ 的等价无穷小
根据题意,${x}^{2}\ln (1+{x}^{2})$ 是 $\sin^nx$ 的高阶无穷小,而 $\sin^nx$ 又是 $1-\cos x$ 的高阶无穷小。因此,$\sin^nx$ 必须是 $x^3$ 的等价无穷小,即 $n=3$。
当 $x \to 0$ 时,$\ln(1+x^2)$ 可以用泰勒展开式近似为 $x^2$,因此 ${x}^{2}\ln (1+{x}^{2})$ 等价于 $x^4$。
步骤 2:确定 $1-\cos x$ 的等价无穷小
当 $x \to 0$ 时,$1-\cos x$ 可以用泰勒展开式近似为 $\frac{x^2}{2}$。
步骤 3:确定 $\sin^nx$ 的等价无穷小
根据题意,${x}^{2}\ln (1+{x}^{2})$ 是 $\sin^nx$ 的高阶无穷小,而 $\sin^nx$ 又是 $1-\cos x$ 的高阶无穷小。因此,$\sin^nx$ 必须是 $x^3$ 的等价无穷小,即 $n=3$。