8.设 =(x)^3+(y)^3+(z)^3-3xyz, 试问在怎样的点集上gradu分别满足:-|||-(1)垂直于z轴;-|||-(2)平行于z轴;-|||-(3)恒为零向量.-|||-9.设f(x,y)可微,l是R^2上的一个确定向量.倘若处处有 _(1)(x,y)=0, 试问此函数f有何特征?-|||-10.设f(x,y)可微,l1与l2是R^2上的一组线性无关向量.试证明:若 _(i)(x,y)=0(i=1,2), 则-|||-f(x,y)= 常数.

题目解答
答案
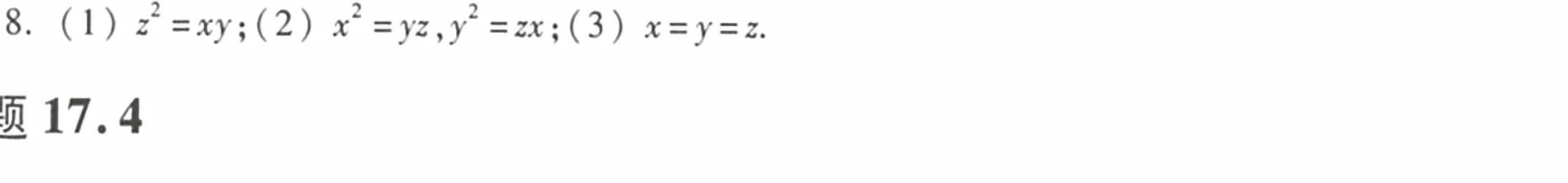
解析
第8题:考查梯度向量的几何意义及偏导数的计算。关键点在于理解梯度向量与坐标轴方向的关系,通过偏导数为零的条件建立方程,求解点集。
第9题:考查方向导数与梯度的关系。核心思路是若梯度与固定向量$l$垂直,则$f$在$l$方向上的变化率为零,说明$f$仅依赖于与$l$垂直的变量组合。
第10题:考查方向导数与梯度的关系及线性无关向量的性质。破题关键是利用线性无关向量张成空间,若所有方向的方向导数为零,则梯度必为零,从而$f$为常数。
第8题
(1) 梯度垂直于z轴
梯度向量$\nabla u$垂直于z轴,当且仅当其z分量为零:
$\frac{\partial u}{\partial z} = 3z^2 - 3xy = 0 \implies z^2 = xy.$
(2) 梯度平行于z轴
梯度向量平行于z轴,当且仅当x、y分量为零:
$\begin{cases}\frac{\partial u}{\partial x} = 3x^2 - 3yz = 0 \implies x^2 = yz, \\\frac{\partial u}{\partial y} = 3y^2 - 3xz = 0 \implies y^2 = xz.\end{cases}$
(3) 梯度恒为零向量
所有偏导数为零:
$\begin{cases}3x^2 - 3yz = 0, \\3y^2 - 3xz = 0, \\3z^2 - 3xy = 0.\end{cases}$
解得$x = y = z$。
第9题
若$\nabla f \cdot l = 0$处处成立,则$f$在$l$方向上的方向导数为零,说明$f$沿$l$方向不变。因此,$f$仅依赖于与$l$垂直的变量组合。
第10题
因$l_1, l_2$线性无关,方向导数在两个方向上为零,说明梯度$\nabla f = 0$。由微分中值定理,$f$为常数。