题目
曲面=2(x)^2+3(y)^2在点 ( 1 , 1 , 5 ) 处的切平面方程为（ ） A , 4 x + 3 y - z = 5 ; B , 4 x + 6 y - z = 5 ; C , 4 x + 3 y - z = 3 ; D , 4 x + 6 y - z = 2
曲面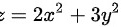
在点 ( 1 , 1 , 5 ) 处的切平面方程为（ ）
A , 4 x + 3 y - z = 5 ;
B , 4 x + 6 y - z = 5 ;
C , 4 x + 3 y - z = 3 ;
D , 4 x + 6 y - z = 2
题目解答
答案
解：另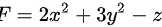
，则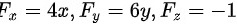
带入 ( 1 , 1 , 5 )可得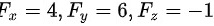
故法向量为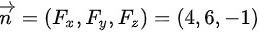
∴切平面方程为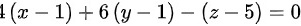
即4x+6y-z=5
故答案为B
解析
步骤 1：定义函数
定义函数$F(x,y,z)=2{x}^{2}+3{y}^{2}-z$，该函数表示曲面$z=2{x}^{2}+3{y}^{2}$。
步骤 2：计算偏导数
计算函数$F(x,y,z)$在点(1,1,5)处的偏导数${F}_{x}$, ${F}_{y}$, ${F}_{z}$。
${F}_{x}=4x$，${F}_{y}=6y$，${F}_{z}=-1$。
步骤 3：代入点(1,1,5)
将点(1,1,5)代入偏导数中，得到${F}_{x}=4$，${F}_{y}=6$，${F}_{z}=-1$。
步骤 4：确定法向量
法向量$\overrightarrow{n}=({F}_{x},{F}_{y},{F}_{z})=(4,6,-1)$。
步骤 5：写出切平面方程
切平面方程为$4(x-1)+6(y-1)-(z-5)=0$，化简得$4x+6y-z=5$。
定义函数$F(x,y,z)=2{x}^{2}+3{y}^{2}-z$，该函数表示曲面$z=2{x}^{2}+3{y}^{2}$。
步骤 2：计算偏导数
计算函数$F(x,y,z)$在点(1,1,5)处的偏导数${F}_{x}$, ${F}_{y}$, ${F}_{z}$。
${F}_{x}=4x$，${F}_{y}=6y$，${F}_{z}=-1$。
步骤 3：代入点(1,1,5)
将点(1,1,5)代入偏导数中，得到${F}_{x}=4$，${F}_{y}=6$，${F}_{z}=-1$。
步骤 4：确定法向量
法向量$\overrightarrow{n}=({F}_{x},{F}_{y},{F}_{z})=(4,6,-1)$。
步骤 5：写出切平面方程
切平面方程为$4(x-1)+6(y-1)-(z-5)=0$，化简得$4x+6y-z=5$。