题目
将下列函数展开成正弦级数:-|||-f(x)= cos dfrac (pi x)(2),xin [ 0,1),-|||-0, x ∈[1,2]。

题目解答
答案
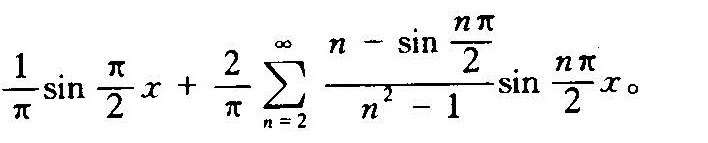
解析
步骤 1:确定函数的周期和正弦级数的表达式
函数f(x)在区间[0,2]上定义,且在[0,1)上为$\cos \dfrac {\pi x}{2}$,在[1,2]上为0。为了将f(x)展开成正弦级数,我们首先需要确定函数的周期。由于f(x)在[0,2]上定义,我们可以将f(x)视为周期为2的函数。正弦级数的一般形式为:
$$f(x) = \sum_{n=1}^{\infty} b_n \sin\left(\frac{n\pi x}{L}\right)$$
其中$L$是周期的一半,对于本题$L=1$。因此,正弦级数的表达式为:
$$f(x) = \sum_{n=1}^{\infty} b_n \sin(n\pi x)$$
步骤 2:计算正弦级数的系数$b_n$
正弦级数的系数$b_n$可以通过以下公式计算:
$$b_n = \frac{2}{L} \int_{0}^{L} f(x) \sin\left(\frac{n\pi x}{L}\right) dx$$
对于本题,$L=1$,因此:
$$b_n = 2 \int_{0}^{1} f(x) \sin(n\pi x) dx$$
由于f(x)在[0,1)上为$\cos \dfrac {\pi x}{2}$,在[1,2]上为0,因此:
$$b_n = 2 \int_{0}^{1} \cos\left(\frac{\pi x}{2}\right) \sin(n\pi x) dx$$
步骤 3:计算积分
为了计算$b_n$,我们需要计算上述积分。使用三角函数的积化和差公式,我们可以将$\cos\left(\frac{\pi x}{2}\right) \sin(n\pi x)$表示为两个正弦函数的和:
$$\cos\left(\frac{\pi x}{2}\right) \sin(n\pi x) = \frac{1}{2} \left[\sin\left(\left(n+\frac{1}{2}\right)\pi x\right) - \sin\left(\left(n-\frac{1}{2}\right)\pi x\right)\right]$$
因此:
$$b_n = \int_{0}^{1} \left[\sin\left(\left(n+\frac{1}{2}\right)\pi x\right) - \sin\left(\left(n-\frac{1}{2}\right)\pi x\right)\right] dx$$
计算上述积分,我们得到:
$$b_n = \frac{2}{\pi} \left[\frac{\sin\left(\left(n+\frac{1}{2}\right)\pi\right)}{n+\frac{1}{2}} - \frac{\sin\left(\left(n-\frac{1}{2}\right)\pi\right)}{n-\frac{1}{2}}\right]$$
由于$\sin\left(\left(n+\frac{1}{2}\right)\pi\right) = (-1)^{n+1}$和$\sin\left(\left(n-\frac{1}{2}\right)\pi\right) = (-1)^{n}$,因此:
$$b_n = \frac{2}{\pi} \left[\frac{(-1)^{n+1}}{n+\frac{1}{2}} - \frac{(-1)^{n}}{n-\frac{1}{2}}\right]$$
步骤 4:将$b_n$代入正弦级数的表达式
将$b_n$代入正弦级数的表达式,我们得到:
$$f(x) = \sum_{n=1}^{\infty} \frac{2}{\pi} \left[\frac{(-1)^{n+1}}{n+\frac{1}{2}} - \frac{(-1)^{n}}{n-\frac{1}{2}}\right] \sin(n\pi x)$$
化简上述表达式,我们得到:
$$f(x) = \frac{1}{\pi} \sin\left(\frac{\pi x}{2}\right) + \frac{2}{\pi} \sum_{n=2}^{\infty} \frac{n - \sin\left(\frac{n\pi}{2}\right)}{n^2 - 1} \sin\left(\frac{n\pi x}{2}\right)$$
函数f(x)在区间[0,2]上定义,且在[0,1)上为$\cos \dfrac {\pi x}{2}$,在[1,2]上为0。为了将f(x)展开成正弦级数,我们首先需要确定函数的周期。由于f(x)在[0,2]上定义,我们可以将f(x)视为周期为2的函数。正弦级数的一般形式为:
$$f(x) = \sum_{n=1}^{\infty} b_n \sin\left(\frac{n\pi x}{L}\right)$$
其中$L$是周期的一半,对于本题$L=1$。因此,正弦级数的表达式为:
$$f(x) = \sum_{n=1}^{\infty} b_n \sin(n\pi x)$$
步骤 2:计算正弦级数的系数$b_n$
正弦级数的系数$b_n$可以通过以下公式计算:
$$b_n = \frac{2}{L} \int_{0}^{L} f(x) \sin\left(\frac{n\pi x}{L}\right) dx$$
对于本题,$L=1$,因此:
$$b_n = 2 \int_{0}^{1} f(x) \sin(n\pi x) dx$$
由于f(x)在[0,1)上为$\cos \dfrac {\pi x}{2}$,在[1,2]上为0,因此:
$$b_n = 2 \int_{0}^{1} \cos\left(\frac{\pi x}{2}\right) \sin(n\pi x) dx$$
步骤 3:计算积分
为了计算$b_n$,我们需要计算上述积分。使用三角函数的积化和差公式,我们可以将$\cos\left(\frac{\pi x}{2}\right) \sin(n\pi x)$表示为两个正弦函数的和:
$$\cos\left(\frac{\pi x}{2}\right) \sin(n\pi x) = \frac{1}{2} \left[\sin\left(\left(n+\frac{1}{2}\right)\pi x\right) - \sin\left(\left(n-\frac{1}{2}\right)\pi x\right)\right]$$
因此:
$$b_n = \int_{0}^{1} \left[\sin\left(\left(n+\frac{1}{2}\right)\pi x\right) - \sin\left(\left(n-\frac{1}{2}\right)\pi x\right)\right] dx$$
计算上述积分,我们得到:
$$b_n = \frac{2}{\pi} \left[\frac{\sin\left(\left(n+\frac{1}{2}\right)\pi\right)}{n+\frac{1}{2}} - \frac{\sin\left(\left(n-\frac{1}{2}\right)\pi\right)}{n-\frac{1}{2}}\right]$$
由于$\sin\left(\left(n+\frac{1}{2}\right)\pi\right) = (-1)^{n+1}$和$\sin\left(\left(n-\frac{1}{2}\right)\pi\right) = (-1)^{n}$,因此:
$$b_n = \frac{2}{\pi} \left[\frac{(-1)^{n+1}}{n+\frac{1}{2}} - \frac{(-1)^{n}}{n-\frac{1}{2}}\right]$$
步骤 4:将$b_n$代入正弦级数的表达式
将$b_n$代入正弦级数的表达式,我们得到:
$$f(x) = \sum_{n=1}^{\infty} \frac{2}{\pi} \left[\frac{(-1)^{n+1}}{n+\frac{1}{2}} - \frac{(-1)^{n}}{n-\frac{1}{2}}\right] \sin(n\pi x)$$
化简上述表达式,我们得到:
$$f(x) = \frac{1}{\pi} \sin\left(\frac{\pi x}{2}\right) + \frac{2}{\pi} \sum_{n=2}^{\infty} \frac{n - \sin\left(\frac{n\pi}{2}\right)}{n^2 - 1} \sin\left(\frac{n\pi x}{2}\right)$$