题目
设事件A与B相互独立，已知P(A)=0.4，(Acup B)=0.7，试求P(B|A).
设事件A与B相互独立，已知$$P(A)=0.4$$，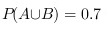
，试求$$P(B|A)$$.
题目解答
答案
$$\because$$A和B相互独立，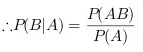
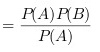$$=P(B)$$
而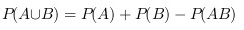
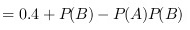
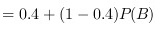
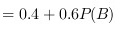
$$=0.7$$
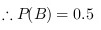
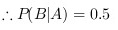
解析
步骤 1：利用事件A与B相互独立的性质
由于事件A与B相互独立，根据概率论中的独立事件性质，我们有$P(AB) = P(A)P(B)$。同时，根据条件概率的定义，$P(B|A) = \dfrac{P(AB)}{P(A)}$。因此，$P(B|A) = \dfrac{P(A)P(B)}{P(A)} = P(B)$。
步骤 2：利用事件A与B的并集概率公式
根据概率论中的并集概率公式，$P(A\cup B) = P(A) + P(B) - P(AB)$。由于A与B相互独立，$P(AB) = P(A)P(B)$，所以$P(A\cup B) = P(A) + P(B) - P(A)P(B)$。将已知的$P(A) = 0.4$和$P(A\cup B) = 0.7$代入，得到$0.7 = 0.4 + P(B) - 0.4P(B)$。
步骤 3：求解$P(B)$
从步骤2的等式$0.7 = 0.4 + P(B) - 0.4P(B)$中，可以解出$P(B)$。首先，将等式整理为$0.7 = 0.4 + 0.6P(B)$，然后解得$P(B) = \dfrac{0.7 - 0.4}{0.6} = \dfrac{0.3}{0.6} = 0.5$。
步骤 4：计算$P(B|A)$
根据步骤1的结论，$P(B|A) = P(B)$，所以$P(B|A) = 0.5$。
由于事件A与B相互独立，根据概率论中的独立事件性质，我们有$P(AB) = P(A)P(B)$。同时，根据条件概率的定义，$P(B|A) = \dfrac{P(AB)}{P(A)}$。因此，$P(B|A) = \dfrac{P(A)P(B)}{P(A)} = P(B)$。
步骤 2：利用事件A与B的并集概率公式
根据概率论中的并集概率公式，$P(A\cup B) = P(A) + P(B) - P(AB)$。由于A与B相互独立，$P(AB) = P(A)P(B)$，所以$P(A\cup B) = P(A) + P(B) - P(A)P(B)$。将已知的$P(A) = 0.4$和$P(A\cup B) = 0.7$代入，得到$0.7 = 0.4 + P(B) - 0.4P(B)$。
步骤 3：求解$P(B)$
从步骤2的等式$0.7 = 0.4 + P(B) - 0.4P(B)$中，可以解出$P(B)$。首先，将等式整理为$0.7 = 0.4 + 0.6P(B)$，然后解得$P(B) = \dfrac{0.7 - 0.4}{0.6} = \dfrac{0.3}{0.6} = 0.5$。
步骤 4：计算$P(B|A)$
根据步骤1的结论，$P(B|A) = P(B)$，所以$P(B|A) = 0.5$。