题目
求下列函数的极值1、(x,y)=6x-(x)^2-4(y)^2+16y-2
求下列函数的极值
1、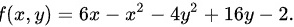
题目解答
答案
已知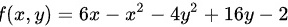 ,得
,得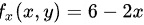 ,
,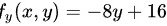 ,通过
,通过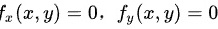 得到极值点为
得到极值点为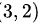 ,同时得到
,同时得到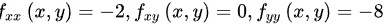 ,令
,令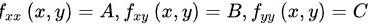 ,将极值点代入可以得到
,将极值点代入可以得到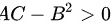 0" data-width="116" data-height="25" data-size="1332" data-format="png" style="max-width:100%">且
0" data-width="116" data-height="25" data-size="1332" data-format="png" style="max-width:100%">且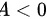 故此点为极大值点,代入原函数可以得到
故此点为极大值点,代入原函数可以得到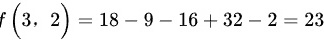 ,故极大值为23.
,故极大值为23.
解析
步骤 1:求偏导数
首先,我们需要求出函数$f(x,y)=6x-{x}^{2}-4{y}^{2}+16y-2$的偏导数。对于$x$的偏导数${f}_{x}(x,y)$,我们有:
$${f}_{x}(x,y)=\frac{\partial f}{\partial x}=6-2x$$
对于$y$的偏导数${f}_{y}(x,y)$,我们有:
$${f}_{y}(x,y)=\frac{\partial f}{\partial y}=-8y+16$$
步骤 2:求极值点
为了找到极值点,我们需要解方程组${f}_{x}(x,y)=0$和${f}_{y}(x,y)=0$。解这个方程组,我们得到:
$$6-2x=0$$
$$-8y+16=0$$
解得$x=3$,$y=2$。因此,极值点为$(3,2)$。
步骤 3:判断极值点的性质
为了判断极值点的性质,我们需要计算二阶偏导数,并使用Hessian矩阵的行列式来判断。二阶偏导数为:
$${f}_{xx}(x,y)=\frac{{\partial}^{2}f}{\partial{x}^{2}}=-2$$
$${f}_{yy}(x,y)=\frac{{\partial}^{2}f}{\partial{y}^{2}}=-8$$
$${f}_{xy}(x,y)=\frac{{\partial}^{2}f}{\partial x\partial y}=0$$
Hessian矩阵的行列式为:
$$D={f}_{xx}{f}_{yy}-{f}_{xy}^{2}=(-2)(-8)-0^{2}=16$$
因为$D>0$且${f}_{xx}<0$,所以极值点$(3,2)$为极大值点。
步骤 4:计算极大值
将极值点$(3,2)$代入原函数$f(x,y)$,我们得到:
$$f(3,2)=6(3)-(3)^{2}-4(2)^{2}+16(2)-2=18-9-16+32-2=23$$
首先,我们需要求出函数$f(x,y)=6x-{x}^{2}-4{y}^{2}+16y-2$的偏导数。对于$x$的偏导数${f}_{x}(x,y)$,我们有:
$${f}_{x}(x,y)=\frac{\partial f}{\partial x}=6-2x$$
对于$y$的偏导数${f}_{y}(x,y)$,我们有:
$${f}_{y}(x,y)=\frac{\partial f}{\partial y}=-8y+16$$
步骤 2:求极值点
为了找到极值点,我们需要解方程组${f}_{x}(x,y)=0$和${f}_{y}(x,y)=0$。解这个方程组,我们得到:
$$6-2x=0$$
$$-8y+16=0$$
解得$x=3$,$y=2$。因此,极值点为$(3,2)$。
步骤 3:判断极值点的性质
为了判断极值点的性质,我们需要计算二阶偏导数,并使用Hessian矩阵的行列式来判断。二阶偏导数为:
$${f}_{xx}(x,y)=\frac{{\partial}^{2}f}{\partial{x}^{2}}=-2$$
$${f}_{yy}(x,y)=\frac{{\partial}^{2}f}{\partial{y}^{2}}=-8$$
$${f}_{xy}(x,y)=\frac{{\partial}^{2}f}{\partial x\partial y}=0$$
Hessian矩阵的行列式为:
$$D={f}_{xx}{f}_{yy}-{f}_{xy}^{2}=(-2)(-8)-0^{2}=16$$
因为$D>0$且${f}_{xx}<0$,所以极值点$(3,2)$为极大值点。
步骤 4:计算极大值
将极值点$(3,2)$代入原函数$f(x,y)$,我们得到:
$$f(3,2)=6(3)-(3)^{2}-4(2)^{2}+16(2)-2=18-9-16+32-2=23$$