题目
求指导本题解题过程,谢谢您!3.求过点(1,2,1)且垂直于直线 ) x-y+z-2=0 x+2y-z+3=0 . 的平面方程.
求指导本题解题过程,谢谢您!
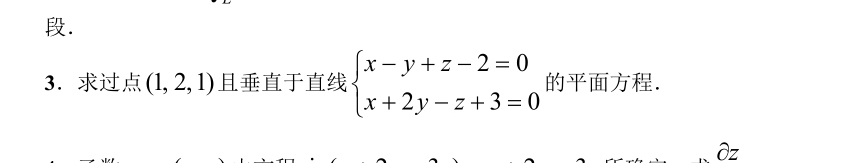
题目解答
答案

解析
考查要点:本题主要考查如何利用两平面交线的方向向量确定所求平面的法向量,并结合已知点写出平面方程。
解题核心思路:
- 确定直线方向向量:题目中直线是两平面的交线,其方向向量由两平面法向量的叉乘得到。
- 构造平面法向量:所求平面垂直于该直线,因此其法向量即为直线的方向向量。
- 代入点法式方程:利用已知点和法向量,写出平面方程。
破题关键点:
- 正确计算两平面法向量的叉乘,得到直线方向向量。
- 验证方程是否满足已知点,确保计算无误。
步骤1:求两平面的法向量
- 第一平面 $x - y + z - 2 = 0$ 的法向量为 $\overrightarrow{n_1} = (1, -1, 1)$。
- 第二平面 $x + 2y - z + 3 = 0$ 的法向量为 $\overrightarrow{n_2} = (1, 2, -1)$。
步骤2:求直线方向向量
直线方向向量 $\overrightarrow{S}$ 为 $\overrightarrow{n_1} \times \overrightarrow{n_2}$:
$\overrightarrow{S} =
\begin{vmatrix}\overrightarrow{i} & \overrightarrow{j} & \overrightarrow{k} \\1 & -1 & 1 \\1 & 2 & -1\end{vmatrix}
= (-1)\overrightarrow{i} + 2\overrightarrow{j} + 3\overrightarrow{k} = (-1, 2, 3)$
步骤3:确定平面方程
所求平面法向量为 $\overrightarrow{S} = (-1, 2, 3)$,过点 $(1, 2, 1)$,代入点法式方程:
$-1(x-1) + 2(y-2) + 3(z-1) = 0$
展开整理得:
$-x + 1 + 2y - 4 + 3z - 3 = 0 \quad \Rightarrow \quad -x + 2y + 3z - 6 = 0$