题目
将函数 (x)=dfrac (1)(x) 展开成 (x-3) 的幂级数.

题目解答
答案
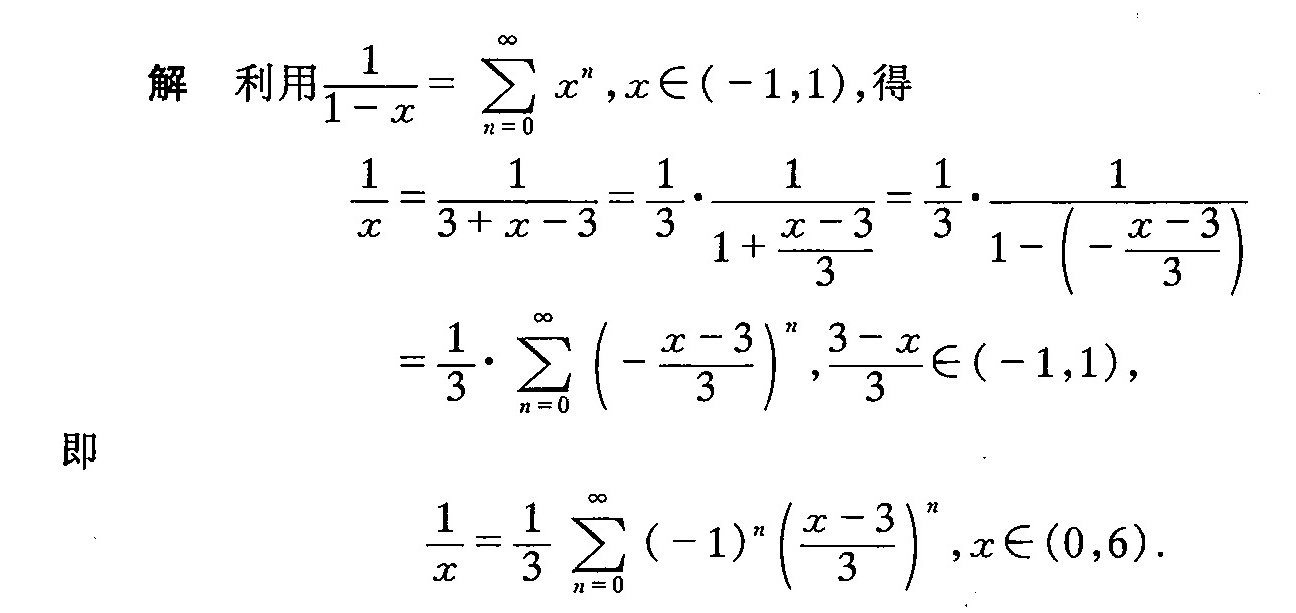
解析
步骤 1:将函数 $f(x)=\dfrac {1}{x}$ 转换为以 $(x-3)$ 为变量的形式
为了将函数 $f(x)=\dfrac {1}{x}$ 展开成 $(x-3)$ 的幂级数,我们首先需要将函数转换为以 $(x-3)$ 为变量的形式。为此,我们可以通过代数变换将 $x$ 表示为 $(x-3)$ 的函数。具体地,我们有 $x = (x-3) + 3$。因此,函数可以写为 $f(x) = \dfrac{1}{(x-3) + 3}$。
步骤 2:将函数写成几何级数的形式
接下来,我们利用几何级数的公式 $\dfrac{1}{1-r} = \sum_{n=0}^{\infty} r^n$,其中 $|r| < 1$。为了将函数写成几何级数的形式,我们需要将分母写成 $1-r$ 的形式。为此,我们有 $f(x) = \dfrac{1}{3} \cdot \dfrac{1}{1 - \left(-\dfrac{x-3}{3}\right)}$。现在,我们已经将函数写成几何级数的形式,其中 $r = -\dfrac{x-3}{3}$。
步骤 3:将函数展开成幂级数
现在,我们可以将函数展开成幂级数。根据几何级数的公式,我们有 $f(x) = \dfrac{1}{3} \sum_{n=0}^{\infty} \left(-\dfrac{x-3}{3}\right)^n$。因此,函数 $f(x)=\dfrac {1}{x}$ 可以展开成 $(x-3)$ 的幂级数。
为了将函数 $f(x)=\dfrac {1}{x}$ 展开成 $(x-3)$ 的幂级数,我们首先需要将函数转换为以 $(x-3)$ 为变量的形式。为此,我们可以通过代数变换将 $x$ 表示为 $(x-3)$ 的函数。具体地,我们有 $x = (x-3) + 3$。因此,函数可以写为 $f(x) = \dfrac{1}{(x-3) + 3}$。
步骤 2:将函数写成几何级数的形式
接下来,我们利用几何级数的公式 $\dfrac{1}{1-r} = \sum_{n=0}^{\infty} r^n$,其中 $|r| < 1$。为了将函数写成几何级数的形式,我们需要将分母写成 $1-r$ 的形式。为此,我们有 $f(x) = \dfrac{1}{3} \cdot \dfrac{1}{1 - \left(-\dfrac{x-3}{3}\right)}$。现在,我们已经将函数写成几何级数的形式,其中 $r = -\dfrac{x-3}{3}$。
步骤 3:将函数展开成幂级数
现在,我们可以将函数展开成幂级数。根据几何级数的公式,我们有 $f(x) = \dfrac{1}{3} \sum_{n=0}^{\infty} \left(-\dfrac{x-3}{3}\right)^n$。因此,函数 $f(x)=\dfrac {1}{x}$ 可以展开成 $(x-3)$ 的幂级数。