题目
5、微分方程 ''-2y'=(x)^2+(e)^2x+1 的待定系数法确定的特解形式(不必求出系数)

题目解答
答案
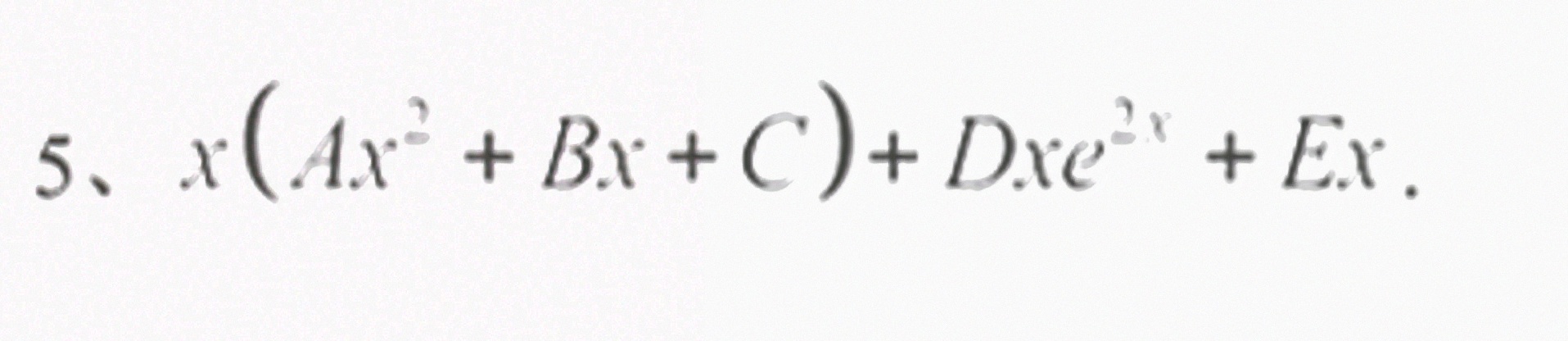
解析
步骤 1:确定齐次方程的解
首先,我们考虑齐次方程 $y''-2y'=0$。特征方程为 $r^2-2r=0$,解得 $r=0$ 或 $r=2$。因此,齐次方程的通解为 $y_h=C_1+C_2e^{2x}$。
步骤 2:确定非齐次方程的特解形式
对于非齐次方程 $y''-2y'={x}^{2}+{e}^{2x}+1$,我们使用待定系数法来确定特解形式。由于非齐次项包含 $x^2$,$e^{2x}$ 和常数项,我们需要分别考虑这些项的特解形式。
- 对于 $x^2$,特解形式为 $Ax^2+Bx+C$。
- 对于 $e^{2x}$,由于 $e^{2x}$ 是齐次方程的解,特解形式为 $Dxe^{2x}$。
- 对于常数项 $1$,特解形式为 $Ex$。
步骤 3:组合特解形式
将上述特解形式组合起来,得到非齐次方程的特解形式为 $y_p=x(Ax^2+Bx+C)+Dxe^{2x}+Ex$。
首先,我们考虑齐次方程 $y''-2y'=0$。特征方程为 $r^2-2r=0$,解得 $r=0$ 或 $r=2$。因此,齐次方程的通解为 $y_h=C_1+C_2e^{2x}$。
步骤 2:确定非齐次方程的特解形式
对于非齐次方程 $y''-2y'={x}^{2}+{e}^{2x}+1$,我们使用待定系数法来确定特解形式。由于非齐次项包含 $x^2$,$e^{2x}$ 和常数项,我们需要分别考虑这些项的特解形式。
- 对于 $x^2$,特解形式为 $Ax^2+Bx+C$。
- 对于 $e^{2x}$,由于 $e^{2x}$ 是齐次方程的解,特解形式为 $Dxe^{2x}$。
- 对于常数项 $1$,特解形式为 $Ex$。
步骤 3:组合特解形式
将上述特解形式组合起来,得到非齐次方程的特解形式为 $y_p=x(Ax^2+Bx+C)+Dxe^{2x}+Ex$。