题目
(3) lim _(narrow infty )dfrac (sqrt {{n)^2-3n}}(2n+1)
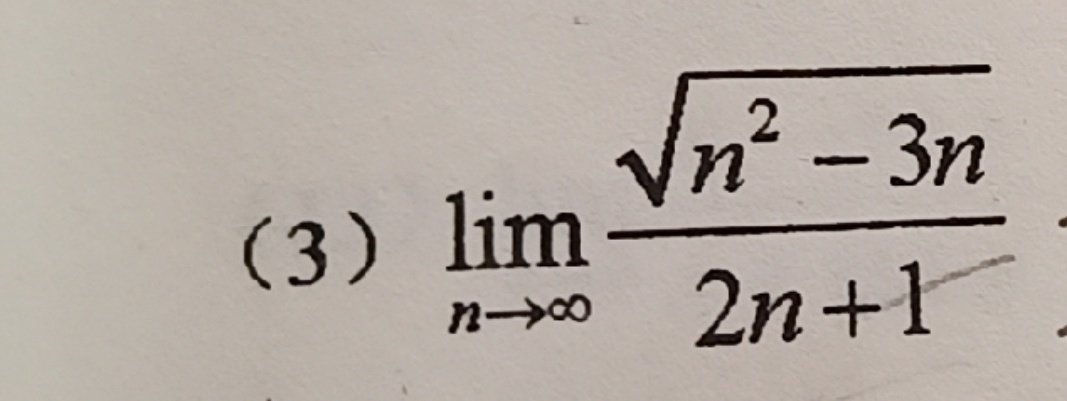
题目解答
答案

解析
步骤 1:确定极限表达式
假设问题要求计算极限 $\lim_{n \to \infty} \frac{\sqrt{n^2 - 3n}}{2n + 1}$。
步骤 2:简化极限表达式
将分子和分母同时除以$n$,得到 $\lim_{n \to \infty} \frac{\sqrt{1 - \frac{3}{n}}}{2 + \frac{1}{n}}$。
步骤 3:计算极限
当$n$趋向于无穷大时,$\frac{3}{n}$和$\frac{1}{n}$都趋向于0,因此极限值为 $\frac{\sqrt{1 - 0}}{2 + 0} = \frac{1}{2}$。
假设问题要求计算极限 $\lim_{n \to \infty} \frac{\sqrt{n^2 - 3n}}{2n + 1}$。
步骤 2:简化极限表达式
将分子和分母同时除以$n$,得到 $\lim_{n \to \infty} \frac{\sqrt{1 - \frac{3}{n}}}{2 + \frac{1}{n}}$。
步骤 3:计算极限
当$n$趋向于无穷大时,$\frac{3}{n}$和$\frac{1}{n}$都趋向于0,因此极限值为 $\frac{\sqrt{1 - 0}}{2 + 0} = \frac{1}{2}$。