题目
lim _(xarrow 0)(dfrac (1)(x)-dfrac (1)({e)^x-1})-|||-__;
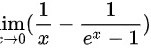 ;
;
题目解答
答案
由等价无穷小替换: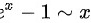 可知
可知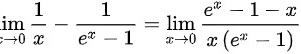
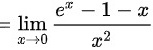
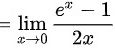 (利用洛必达法则)
(利用洛必达法则)
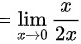 (利用等价无穷小替换:
(利用等价无穷小替换: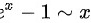 )
)
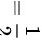
故答案为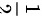 。
。
解析
步骤 1:化简表达式
首先,我们化简给定的极限表达式。我们有:
$$\lim _{x\rightarrow 0}\left(\dfrac {1}{x}-\dfrac {1}{{e}^{x}-1}\right)$$
将两个分数合并为一个分数,得到:
$$\lim _{x\rightarrow 0}\dfrac {{e}^{x}-1-x}{x({e}^{x}-1)}$$
步骤 2:应用洛必达法则
由于直接代入$x=0$会导致分母为0,我们应用洛必达法则。洛必达法则适用于$\frac{0}{0}$或$\frac{\infty}{\infty}$形式的极限。我们对分子和分母分别求导,得到:
$$\lim _{x\rightarrow 0}\dfrac {{e}^{x}-1}{x{e}^{x}}$$
步骤 3:再次应用洛必达法则
由于上述表达式仍然为$\frac{0}{0}$形式,我们再次应用洛必达法则,得到:
$$\lim _{x\rightarrow 0}\dfrac {{e}^{x}}{x{e}^{x}+{e}^{x}}$$
简化得到:
$$\lim _{x\rightarrow 0}\dfrac {1}{x+1}$$
步骤 4:计算极限
现在,我们可以直接代入$x=0$,得到:
$$\lim _{x\rightarrow 0}\dfrac {1}{x+1}=\dfrac {1}{0+1}=\dfrac {1}{1}$$
首先,我们化简给定的极限表达式。我们有:
$$\lim _{x\rightarrow 0}\left(\dfrac {1}{x}-\dfrac {1}{{e}^{x}-1}\right)$$
将两个分数合并为一个分数,得到:
$$\lim _{x\rightarrow 0}\dfrac {{e}^{x}-1-x}{x({e}^{x}-1)}$$
步骤 2:应用洛必达法则
由于直接代入$x=0$会导致分母为0,我们应用洛必达法则。洛必达法则适用于$\frac{0}{0}$或$\frac{\infty}{\infty}$形式的极限。我们对分子和分母分别求导,得到:
$$\lim _{x\rightarrow 0}\dfrac {{e}^{x}-1}{x{e}^{x}}$$
步骤 3:再次应用洛必达法则
由于上述表达式仍然为$\frac{0}{0}$形式,我们再次应用洛必达法则,得到:
$$\lim _{x\rightarrow 0}\dfrac {{e}^{x}}{x{e}^{x}+{e}^{x}}$$
简化得到:
$$\lim _{x\rightarrow 0}\dfrac {1}{x+1}$$
步骤 4:计算极限
现在,我们可以直接代入$x=0$,得到:
$$\lim _{x\rightarrow 0}\dfrac {1}{x+1}=\dfrac {1}{0+1}=\dfrac {1}{1}$$