题目
2.设函数 y=f(x) 是由方程 sin ((x)^2+y)=x 所确定,求dy。
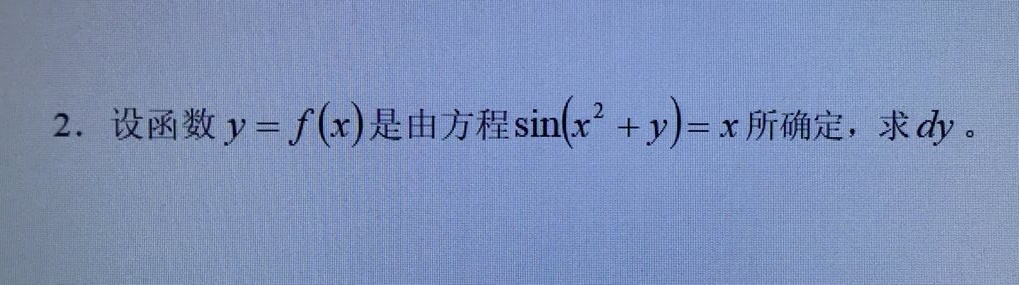
题目解答
答案
等式两边对x求导,左边:cos(x²+y)2xdy/dx,右边等于1,即cos(x²+y)2xdy/dx=1,即dy=dx/2xcos(x²+y),,对的话参考一下,错的话还请见谅
解析
步骤 1:隐函数求导
给定方程 $\sin ({x}^{2}+y)=x$,我们首先对两边同时对 $x$ 求导。根据链式法则,左边的导数为 $\cos({x}^{2}+y) \cdot (2x + \frac{dy}{dx})$,右边的导数为 $1$。
步骤 2:求解 $\frac{dy}{dx}$
将步骤 1 中的导数结果设置为等式,得到 $\cos({x}^{2}+y) \cdot (2x + \frac{dy}{dx}) = 1$。解这个方程以求出 $\frac{dy}{dx}$,即 $\frac{dy}{dx} = \frac{1}{\cos({x}^{2}+y)} - 2x$。
步骤 3:求解 $dy$
$dy$ 是 $\frac{dy}{dx}$ 与 $dx$ 的乘积,即 $dy = \left(\frac{1}{\cos({x}^{2}+y)} - 2x\right)dx$。
给定方程 $\sin ({x}^{2}+y)=x$,我们首先对两边同时对 $x$ 求导。根据链式法则,左边的导数为 $\cos({x}^{2}+y) \cdot (2x + \frac{dy}{dx})$,右边的导数为 $1$。
步骤 2:求解 $\frac{dy}{dx}$
将步骤 1 中的导数结果设置为等式,得到 $\cos({x}^{2}+y) \cdot (2x + \frac{dy}{dx}) = 1$。解这个方程以求出 $\frac{dy}{dx}$,即 $\frac{dy}{dx} = \frac{1}{\cos({x}^{2}+y)} - 2x$。
步骤 3:求解 $dy$
$dy$ 是 $\frac{dy}{dx}$ 与 $dx$ 的乘积,即 $dy = \left(\frac{1}{\cos({x}^{2}+y)} - 2x\right)dx$。