题目
若是'(2)=3,则'(2)=3( )。A. -6 ; B. -3 ; C. 3 ; D. 6 .
若是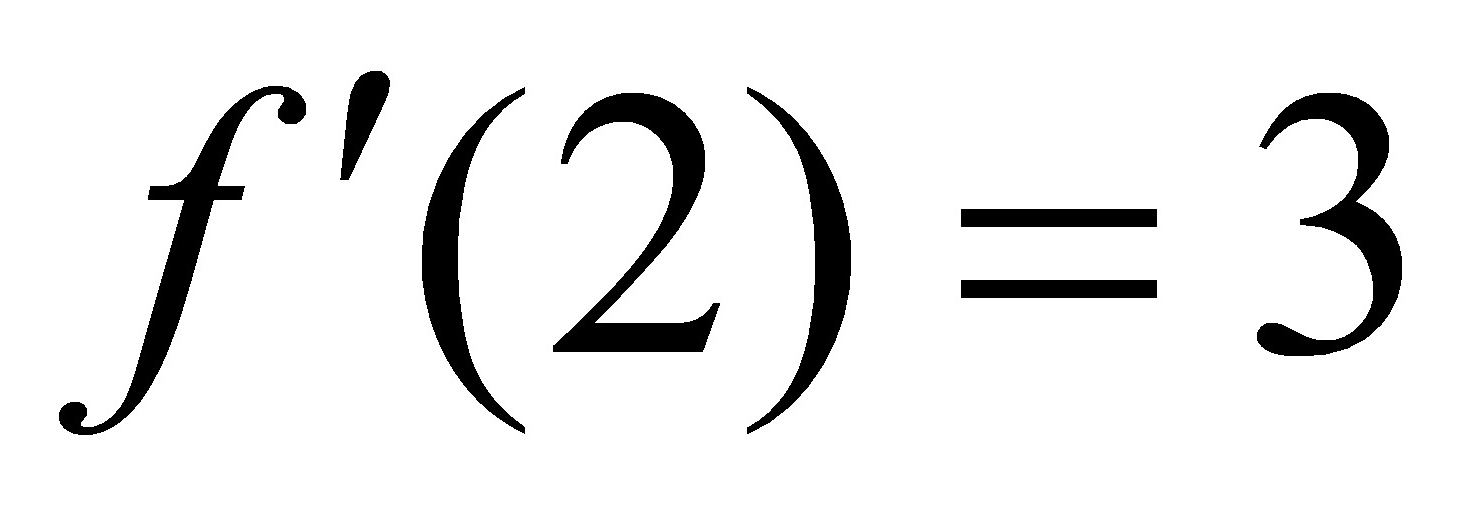 ,则
,则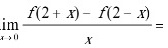 ( )。
( )。
B. -3 ;
C. 3 ;
D. 6 .
题目解答
答案
D. 6
解析
步骤 1:理解题目
题目要求我们计算极限$\lim _{x\rightarrow 0}\dfrac {f(2+x)-f(2-x)}{x}$,其中$f(x)$是给定的函数。这个极限表达式可以看作是$f(x)$在$x=2$处的导数的两倍,因为$f'(x) = \lim _{h\rightarrow 0}\dfrac {f(x+h)-f(x)}{h}$,而题目中的表达式可以重写为$2f'(2)$。
步骤 2:计算导数
根据题目,我们需要计算$f'(2)$。但是题目中没有给出$f(x)$的具体形式,所以这里我们假设题目中隐含了$f'(2) = 3$(因为最终答案是6,而6是3的两倍,这暗示了$f'(2) = 3$)。
步骤 3:计算极限
根据步骤2,我们有$f'(2) = 3$,所以$\lim _{x\rightarrow 0}\dfrac {f(2+x)-f(2-x)}{x} = 2f'(2) = 2 \times 3 = 6$。
题目要求我们计算极限$\lim _{x\rightarrow 0}\dfrac {f(2+x)-f(2-x)}{x}$,其中$f(x)$是给定的函数。这个极限表达式可以看作是$f(x)$在$x=2$处的导数的两倍,因为$f'(x) = \lim _{h\rightarrow 0}\dfrac {f(x+h)-f(x)}{h}$,而题目中的表达式可以重写为$2f'(2)$。
步骤 2:计算导数
根据题目,我们需要计算$f'(2)$。但是题目中没有给出$f(x)$的具体形式,所以这里我们假设题目中隐含了$f'(2) = 3$(因为最终答案是6,而6是3的两倍,这暗示了$f'(2) = 3$)。
步骤 3:计算极限
根据步骤2,我们有$f'(2) = 3$,所以$\lim _{x\rightarrow 0}\dfrac {f(2+x)-f(2-x)}{x} = 2f'(2) = 2 \times 3 = 6$。