题目
求函数(x,y)=(x)^3-(y)^3+3(x)^2+3(y)^2-9x-|||-__的极值
求函数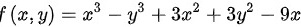 的极值
的极值
题目解答
答案
本题答案为:函数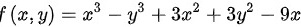 在点
在点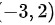 处取得极大值为:
处取得极大值为: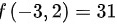
解:由题可得:函数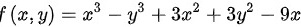
求其一阶偏导数为: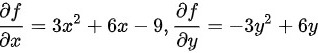
令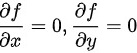
解得: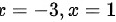 ,
,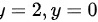
因此函数的驻点为: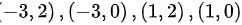
求出该函数的二阶偏导数为: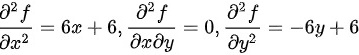
在驻点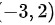 处,有
处,有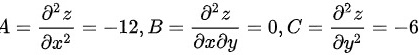
所以有: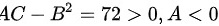 0,A<0" data-width="224" data-height="26" data-size="2875" data-format="png" style="max-width:100%">
0,A<0" data-width="224" data-height="26" data-size="2875" data-format="png" style="max-width:100%">
因此函数在点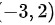 处取得极大值为:
处取得极大值为: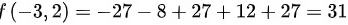
在驻点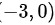 处,有
处,有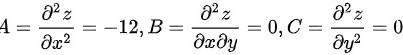
所以有: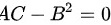
即函数在该点处不取极值;
在驻点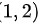 处,有
处,有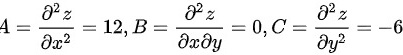
所以有: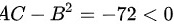
即函数在该点处不取极值;
在驻点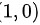 处,有
处,有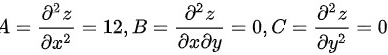
所以有: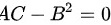
即函数在该点处不取极值;
综上可得:函数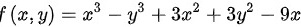 在点
在点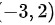 处取得极大值为:
处取得极大值为: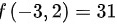
解析
步骤 1:求一阶偏导数
对函数$f(x,y)={x}^{3}-{y}^{3}+3{x}^{2}+3{y}^{2}-9x$求一阶偏导数,得到:
$\dfrac {\partial f}{\partial x}=3{x}^{2}+6x-9$
$\dfrac {\partial f}{\partial y}=-3{y}^{2}+6y$
步骤 2:求驻点
令$\dfrac {\partial f}{\partial x}=0$和$\dfrac {\partial f}{\partial y}=0$,解得:
$3{x}^{2}+6x-9=0$,解得$x=-3$或$x=1$
$-3{y}^{2}+6y=0$,解得$y=0$或$y=2$
因此,函数的驻点为:(-3,2)、(-3,0)、(1,2)、(1,0)
步骤 3:求二阶偏导数
求出该函数的二阶偏导数为:
$\dfrac {{\partial }^{2}f}{\partial {x}^{2}}=6x+6$
$\dfrac {{\partial }^{2}f}{\partial x\partial y}=0$
$\dfrac {{\partial }^{2}f}{\partial {y}^{2}}=-6y+6$
步骤 4:判断极值
在驻点(-3,2)处,有$A=\dfrac {{\partial }^{2}f}{\partial {x}^{2}}=-12$,$B=\dfrac {{\partial }^{2}f}{\partial x\partial y}=0$,$C=\dfrac {{\partial }^{2}f}{\partial {y}^{2}}=-6$
所以有:$AC-{B}^{2}=72>0$,$A<0$
因此函数在点(-3,2)处取得极大值为:$f(-3,2)=-27-8+27+12+27=31$
在驻点(-3,0)处,有$A=\dfrac {{\partial }^{2}f}{\partial {x}^{2}}=-12$,$B=\dfrac {{\partial }^{2}f}{\partial x\partial y}=0$,$C=\dfrac {{\partial }^{2}f}{\partial {y}^{2}}=6$
所以有:$AC-{B}^{2}=0$
即函数在该点处不取极值;
在驻点(1,2)处,有$A=\dfrac {{\partial }^{2}f}{\partial {x}^{2}}=12$,$B=\dfrac {{\partial }^{2}f}{\partial x\partial y}=0$,$C=\dfrac {{\partial }^{2}f}{\partial {y}^{2}}=-6$
所以有:$AC-{B}^{2}=-72<0$
即函数在该点处不取极值;
在驻点(1,0)处,有$A=\dfrac {{\partial }^{2}f}{\partial {x}^{2}}=12$,$B=\dfrac {{\partial }^{2}f}{\partial x\partial y}=0$,$C=\dfrac {{\partial }^{2}f}{\partial {y}^{2}}=6$
所以有:$AC-{B}^{2}=0$
即函数在该点处不取极值;
对函数$f(x,y)={x}^{3}-{y}^{3}+3{x}^{2}+3{y}^{2}-9x$求一阶偏导数,得到:
$\dfrac {\partial f}{\partial x}=3{x}^{2}+6x-9$
$\dfrac {\partial f}{\partial y}=-3{y}^{2}+6y$
步骤 2:求驻点
令$\dfrac {\partial f}{\partial x}=0$和$\dfrac {\partial f}{\partial y}=0$,解得:
$3{x}^{2}+6x-9=0$,解得$x=-3$或$x=1$
$-3{y}^{2}+6y=0$,解得$y=0$或$y=2$
因此,函数的驻点为:(-3,2)、(-3,0)、(1,2)、(1,0)
步骤 3:求二阶偏导数
求出该函数的二阶偏导数为:
$\dfrac {{\partial }^{2}f}{\partial {x}^{2}}=6x+6$
$\dfrac {{\partial }^{2}f}{\partial x\partial y}=0$
$\dfrac {{\partial }^{2}f}{\partial {y}^{2}}=-6y+6$
步骤 4:判断极值
在驻点(-3,2)处,有$A=\dfrac {{\partial }^{2}f}{\partial {x}^{2}}=-12$,$B=\dfrac {{\partial }^{2}f}{\partial x\partial y}=0$,$C=\dfrac {{\partial }^{2}f}{\partial {y}^{2}}=-6$
所以有:$AC-{B}^{2}=72>0$,$A<0$
因此函数在点(-3,2)处取得极大值为:$f(-3,2)=-27-8+27+12+27=31$
在驻点(-3,0)处,有$A=\dfrac {{\partial }^{2}f}{\partial {x}^{2}}=-12$,$B=\dfrac {{\partial }^{2}f}{\partial x\partial y}=0$,$C=\dfrac {{\partial }^{2}f}{\partial {y}^{2}}=6$
所以有:$AC-{B}^{2}=0$
即函数在该点处不取极值;
在驻点(1,2)处,有$A=\dfrac {{\partial }^{2}f}{\partial {x}^{2}}=12$,$B=\dfrac {{\partial }^{2}f}{\partial x\partial y}=0$,$C=\dfrac {{\partial }^{2}f}{\partial {y}^{2}}=-6$
所以有:$AC-{B}^{2}=-72<0$
即函数在该点处不取极值;
在驻点(1,0)处,有$A=\dfrac {{\partial }^{2}f}{\partial {x}^{2}}=12$,$B=\dfrac {{\partial }^{2}f}{\partial x\partial y}=0$,$C=\dfrac {{\partial }^{2}f}{\partial {y}^{2}}=6$
所以有:$AC-{B}^{2}=0$
即函数在该点处不取极值;