题目
已知lim _(xarrow +infty )(x)^a[ sqrt ({x)^2+1}+sqrt ({x)^2-1}-2x] =bneq 0 x]=b≠0，则lim _(xarrow +infty )(x)^a[ sqrt ({x)^2+1}+sqrt ({x)^2-1}-2x] =bneq 0 x]=b≠0为lim _(xarrow +infty )(x)^a[ sqrt ({x)^2+1}+sqrt ({x)^2-1}-2x] =bneq 0 x]=b≠0。lim _(xarrow +infty )(x)^a[ sqrt ({x)^2+1}+sqrt ({x)^2-1}-2x] =bneq 0 x]=b≠0lim _(xarrow +infty )(x)^a[ sqrt ({x)^2+1}+sqrt ({x)^2-1}-2x] =bneq 0 x]=b≠0lim _(xarrow +infty )(x)^a[ sqrt ({x)^2+1}+sqrt ({x)^2-1}-2x] =bneq 0 x]=b≠0lim _(xarrow +infty )(x)^a[ sqrt ({x)^2+1}+sqrt ({x)^2-1}-2x] =bneq 0 x]=b≠0
已知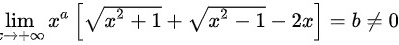
，则
为
。
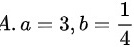
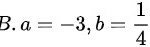
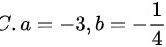
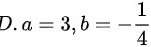
题目解答
答案
由题意知，极限为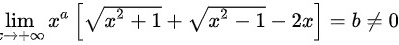，令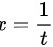
，
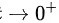，则极限化为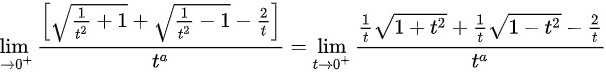
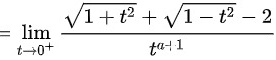，根据泰勒展开式，
时，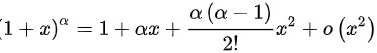
，因此，可以得到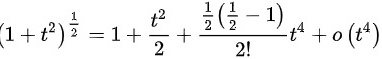
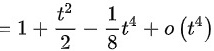
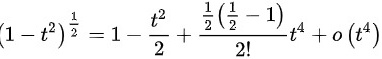
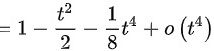，故极限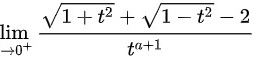
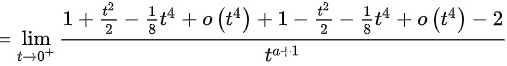
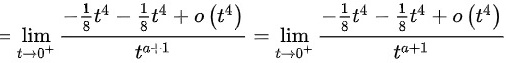
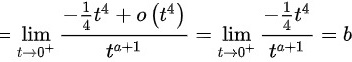结合上下同阶原则，可以得到
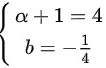，即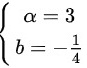
，故正确答案选择
。
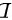解析
步骤 1：变量替换
令 $t = \frac{1}{x}$，则当 $x \rightarrow +\infty$ 时，$t \rightarrow 0^+$。原极限可以写为：
$$\lim _{t\rightarrow {0}^{+}}\dfrac {\sqrt {1+{t}^{2}}+\sqrt {1-{t}^{2}}-2}{{t}^{a+1}}$$
步骤 2：泰勒展开
根据泰勒展开式，当 $t \rightarrow 0$ 时，有：
$${(1+x)}^{\alpha }=1+\alpha x+\dfrac {\alpha (\alpha -1)}{2!}{x}^{2}+o({x}^{2})$$
因此，可以得到：
$${(1+{t}^{2})}^{\dfrac {1}{2}}=1+\dfrac {{t}^{2}}{2}+\dfrac {\dfrac {1}{2}(\dfrac {1}{2}-1)}{2!}{t}^{4}+o({t}^{4})$$
$$=1+\dfrac {{t}^{2}}{2}-\dfrac {1}{8}{t}^{4}+o({t}^{4})$$
$${(1-{t}^{2})}^{\dfrac {1}{2}}=1-\dfrac {{t}^{2}}{2}+\dfrac {\dfrac {1}{2}(\dfrac {1}{2}-1)}{2!}{t}^{4}+o({t}^{4})$$
$$=1-\dfrac {{t}^{2}}{2}-\dfrac {1}{8}{t}^{4}+o({t}^{4})$$
步骤 3：计算极限
将上述泰勒展开式代入原极限，得到：
$$\lim _{t\rightarrow {0}^{+}}\dfrac {\sqrt {1+{t}^{2}}+\sqrt {1-{t}^{2}}-2}{{t}^{a+1}}$$
$$=\lim _{t\rightarrow {0}^{+}}\dfrac {1+\dfrac {{t}^{2}}{2}-\dfrac {1}{8}{t}^{4}+o({t}^{4})+1-\dfrac {{t}^{2}}{2}-\dfrac {1}{8}{t}^{4}+o({t}^{4})-2}{{t}^{a+1}}$$
$$=\lim _{t\rightarrow {0}^{+}}\dfrac {-\dfrac {1}{4}{t}^{4}+o({t}^{4})}{{t}^{a+1}}$$
$$=\lim _{t\rightarrow {0}^{+}}\dfrac {-\dfrac {1}{4}{t}^{4}}{{t}^{a+1}}$$
结合上下同阶原则，可以得到：
$$\left \{ \begin{matrix} a+1=4\\ b=-\dfrac {1}{4}\end{matrix} \right.$$
即：
$$\left \{ \begin{matrix} a=3\\ b=-\dfrac {1}{4}\end{matrix} \right.$$
令 $t = \frac{1}{x}$，则当 $x \rightarrow +\infty$ 时，$t \rightarrow 0^+$。原极限可以写为：
$$\lim _{t\rightarrow {0}^{+}}\dfrac {\sqrt {1+{t}^{2}}+\sqrt {1-{t}^{2}}-2}{{t}^{a+1}}$$
步骤 2：泰勒展开
根据泰勒展开式，当 $t \rightarrow 0$ 时，有：
$${(1+x)}^{\alpha }=1+\alpha x+\dfrac {\alpha (\alpha -1)}{2!}{x}^{2}+o({x}^{2})$$
因此，可以得到：
$${(1+{t}^{2})}^{\dfrac {1}{2}}=1+\dfrac {{t}^{2}}{2}+\dfrac {\dfrac {1}{2}(\dfrac {1}{2}-1)}{2!}{t}^{4}+o({t}^{4})$$
$$=1+\dfrac {{t}^{2}}{2}-\dfrac {1}{8}{t}^{4}+o({t}^{4})$$
$${(1-{t}^{2})}^{\dfrac {1}{2}}=1-\dfrac {{t}^{2}}{2}+\dfrac {\dfrac {1}{2}(\dfrac {1}{2}-1)}{2!}{t}^{4}+o({t}^{4})$$
$$=1-\dfrac {{t}^{2}}{2}-\dfrac {1}{8}{t}^{4}+o({t}^{4})$$
步骤 3：计算极限
将上述泰勒展开式代入原极限，得到：
$$\lim _{t\rightarrow {0}^{+}}\dfrac {\sqrt {1+{t}^{2}}+\sqrt {1-{t}^{2}}-2}{{t}^{a+1}}$$
$$=\lim _{t\rightarrow {0}^{+}}\dfrac {1+\dfrac {{t}^{2}}{2}-\dfrac {1}{8}{t}^{4}+o({t}^{4})+1-\dfrac {{t}^{2}}{2}-\dfrac {1}{8}{t}^{4}+o({t}^{4})-2}{{t}^{a+1}}$$
$$=\lim _{t\rightarrow {0}^{+}}\dfrac {-\dfrac {1}{4}{t}^{4}+o({t}^{4})}{{t}^{a+1}}$$
$$=\lim _{t\rightarrow {0}^{+}}\dfrac {-\dfrac {1}{4}{t}^{4}}{{t}^{a+1}}$$
结合上下同阶原则，可以得到：
$$\left \{ \begin{matrix} a+1=4\\ b=-\dfrac {1}{4}\end{matrix} \right.$$
即：
$$\left \{ \begin{matrix} a=3\\ b=-\dfrac {1}{4}\end{matrix} \right.$$