题目
设第一只盒子中装有3只蓝色球,2只绿色球,2只白色求,第二只盒子中装有2只蓝色球,3只绿色球,4只白色球,独立地分别在两只盒子中各取一只球。(1)求至少有一只蓝色球的概率;(2)求有一只蓝色球,一只白色球的概率;(3)已知至少有一只蓝色球,求有一只蓝色球、一只白色球的概率.
设第一只盒子中装有3只蓝色球,2只绿色球,2只白色求,第二只盒子中装有2只蓝色球,3只绿色球,4只白色球,独立地分别在两只盒子中各取一只球。
(1)求至少有一只蓝色球的概率;
(2)求有一只蓝色球,一只白色球的概率;
(3)已知至少有一只蓝色球,求有一只蓝色球、一只白色球的概率.
题目解答
答案
(1)至少有一只蓝色球的概率为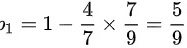 ;
;
(2)有一只蓝色球,一只白色球的概率为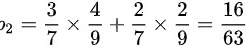 ;
;
(3)已知至少有一只蓝色球,则有一只蓝色球、一只白色球的条件概率为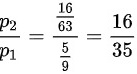 .
.
解析
考查要点:本题主要考查独立事件的概率计算、补集思想的应用、条件概率的理解与计算。
解题核心思路:
- 至少有一个事件发生的概率通常用补集法计算更简便;
- 分类讨论不同事件组合的概率并求和;
- 条件概率公式的应用,需明确事件间的包含关系。
破题关键点:
- 独立事件:两盒子取球互不影响,概率相乘;
- 事件分解:将复杂事件拆解为互斥的简单事件;
- 条件概率:注意分母为已知事件的概率,分子为联合概率。
第(1)题
至少有一只蓝色球的概率
补集法:
- 计算都不取蓝色球的概率:
- 第一盒不取蓝色的概率:$\dfrac{4}{7}$(2绿+2白);
- 第二盒不取蓝色的概率:$\dfrac{7}{9}$(3绿+4白);
- 联合概率:$\dfrac{4}{7} \times \dfrac{7}{9} = \dfrac{4}{9}$。
- 至少一个蓝色的概率:
$1 - \dfrac{4}{9} = \dfrac{5}{9}.$
第(2)题
一只蓝色球,一只白色球的概率
分类讨论:
- 第一盒蓝,第二盒白:
$\dfrac{3}{7} \times \dfrac{4}{9} = \dfrac{12}{63}.$ - 第一盒白,第二盒蓝:
$\dfrac{2}{7} \times \dfrac{2}{9} = \dfrac{4}{63}.$ - 总概率:
$\dfrac{12}{63} + \dfrac{4}{63} = \dfrac{16}{63}.$
第(3)题
条件概率
公式应用:
- 已知事件A(至少一蓝)的概率:$P(A) = \dfrac{5}{9}$;
- 事件B(一蓝一白)的概率:$P(B) = \dfrac{16}{63}$;
- 条件概率:
$P(B|A) = \dfrac{P(B)}{P(A)} = \dfrac{\dfrac{16}{63}}{\dfrac{5}{9}} = \dfrac{16}{35}.$