题目
(6)设 _(n)=dfrac (3)(2)(int )_(0)^dfrac (n{n+1)}(x)^n-1sqrt (1+{x)^n}dx, 则极限limnan等于 ()-|||-(A) ((1+e))^dfrac (3{2)}+1 (B) ((1+{e)^-1)}^dfrac (3{2)}-1-|||-(C) ((1+{e)^-1)}^dfrac (3{2)}+1 (D) ((1+e))^dfrac (3{2)}-1

题目解答
答案
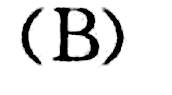
解析
步骤 1:计算积分
首先,我们计算积分 ${\int }_{0}^{\dfrac {n}{n+1}}{x}^{n-1}\sqrt {1+{x}^{n}}dx$。令 $u = 1 + x^n$,则 $du = nx^{n-1}dx$,因此 $x^{n-1}dx = \frac{1}{n}du$。当 $x = 0$ 时,$u = 1$;当 $x = \frac{n}{n+1}$ 时,$u = 1 + \left(\frac{n}{n+1}\right)^n$。因此,积分变为
\[
\int_{1}^{1 + \left(\frac{n}{n+1}\right)^n} \frac{1}{n} \sqrt{u} du = \frac{1}{n} \int_{1}^{1 + \left(\frac{n}{n+1}\right)^n} u^{\frac{1}{2}} du = \frac{1}{n} \left[ \frac{2}{3} u^{\frac{3}{2}} \right]_{1}^{1 + \left(\frac{n}{n+1}\right)^n} = \frac{2}{3n} \left[ \left(1 + \left(\frac{n}{n+1}\right)^n\right)^{\frac{3}{2}} - 1 \right].
\]
步骤 2:计算 ${a}_{n}$
将上述结果代入 ${a}_{n}=\dfrac {3}{2}{\int }_{0}^{\dfrac {n}{n+1}}{x}^{n-1}\sqrt {1+{x}^{n}}dx$,得到
\[
{a}_{n} = \frac{3}{2} \cdot \frac{2}{3n} \left[ \left(1 + \left(\frac{n}{n+1}\right)^n\right)^{\frac{3}{2}} - 1 \right] = \frac{1}{n} \left[ \left(1 + \left(\frac{n}{n+1}\right)^n\right)^{\frac{3}{2}} - 1 \right].
\]
步骤 3:计算极限
计算极限 $\lim_{n \to \infty} n a_n$,得到
\[
\lim_{n \to \infty} n a_n = \lim_{n \to \infty} \left[ \left(1 + \left(\frac{n}{n+1}\right)^n\right)^{\frac{3}{2}} - 1 \right].
\]
由于 $\lim_{n \to \infty} \left(\frac{n}{n+1}\right)^n = \lim_{n \to \infty} \left(1 - \frac{1}{n+1}\right)^n = e^{-1}$,因此
\[
\lim_{n \to \infty} n a_n = \left(1 + e^{-1}\right)^{\frac{3}{2}} - 1.
\]
首先,我们计算积分 ${\int }_{0}^{\dfrac {n}{n+1}}{x}^{n-1}\sqrt {1+{x}^{n}}dx$。令 $u = 1 + x^n$,则 $du = nx^{n-1}dx$,因此 $x^{n-1}dx = \frac{1}{n}du$。当 $x = 0$ 时,$u = 1$;当 $x = \frac{n}{n+1}$ 时,$u = 1 + \left(\frac{n}{n+1}\right)^n$。因此,积分变为
\[
\int_{1}^{1 + \left(\frac{n}{n+1}\right)^n} \frac{1}{n} \sqrt{u} du = \frac{1}{n} \int_{1}^{1 + \left(\frac{n}{n+1}\right)^n} u^{\frac{1}{2}} du = \frac{1}{n} \left[ \frac{2}{3} u^{\frac{3}{2}} \right]_{1}^{1 + \left(\frac{n}{n+1}\right)^n} = \frac{2}{3n} \left[ \left(1 + \left(\frac{n}{n+1}\right)^n\right)^{\frac{3}{2}} - 1 \right].
\]
步骤 2:计算 ${a}_{n}$
将上述结果代入 ${a}_{n}=\dfrac {3}{2}{\int }_{0}^{\dfrac {n}{n+1}}{x}^{n-1}\sqrt {1+{x}^{n}}dx$,得到
\[
{a}_{n} = \frac{3}{2} \cdot \frac{2}{3n} \left[ \left(1 + \left(\frac{n}{n+1}\right)^n\right)^{\frac{3}{2}} - 1 \right] = \frac{1}{n} \left[ \left(1 + \left(\frac{n}{n+1}\right)^n\right)^{\frac{3}{2}} - 1 \right].
\]
步骤 3:计算极限
计算极限 $\lim_{n \to \infty} n a_n$,得到
\[
\lim_{n \to \infty} n a_n = \lim_{n \to \infty} \left[ \left(1 + \left(\frac{n}{n+1}\right)^n\right)^{\frac{3}{2}} - 1 \right].
\]
由于 $\lim_{n \to \infty} \left(\frac{n}{n+1}\right)^n = \lim_{n \to \infty} \left(1 - \frac{1}{n+1}\right)^n = e^{-1}$,因此
\[
\lim_{n \to \infty} n a_n = \left(1 + e^{-1}\right)^{\frac{3}{2}} - 1.
\]