题目
设随机变量X的分布列为 X=k =dfrac (a)({2)^k}(k=1,2,... ).,求:(1)参数a; X=k =dfrac (a)({2)^k}(k=1,2,... ).; X=k =dfrac (a)({2)^k}(k=1,2,... ).的分布列.
设随机变量X的分布列为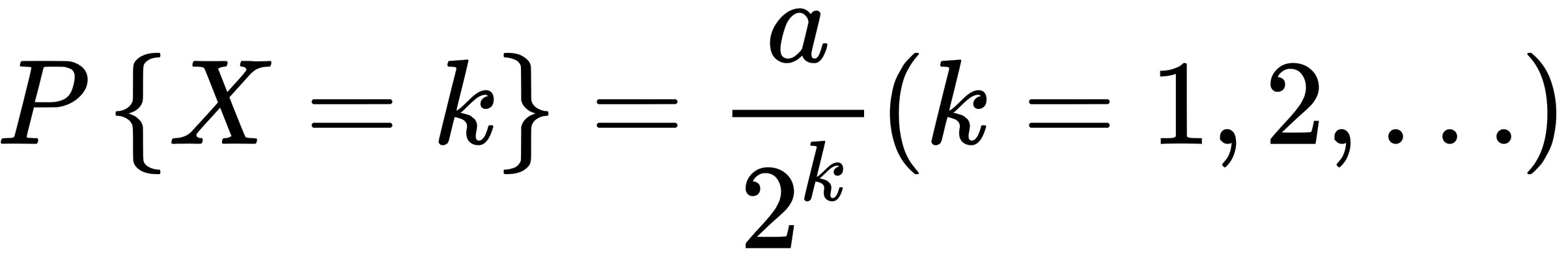 ,求:
,求:
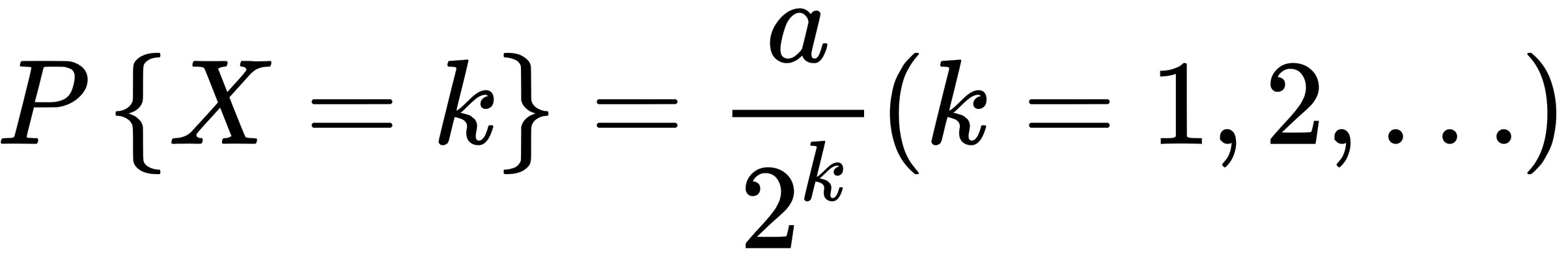 ,求:
,求:(1)参数a;
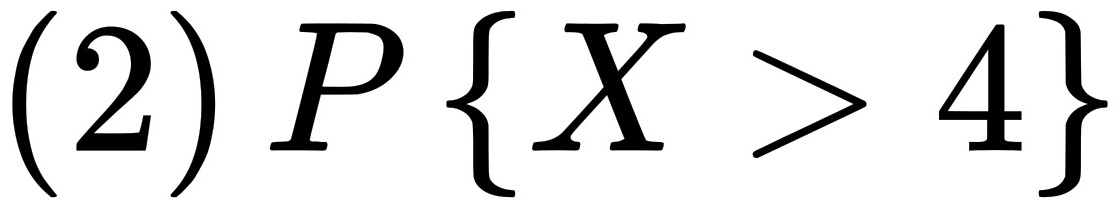 ;
;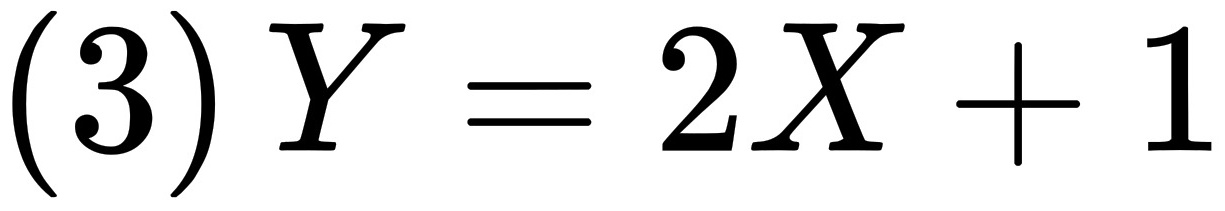 的分布列.
的分布列.题目解答
答案
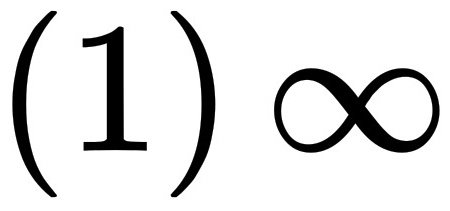

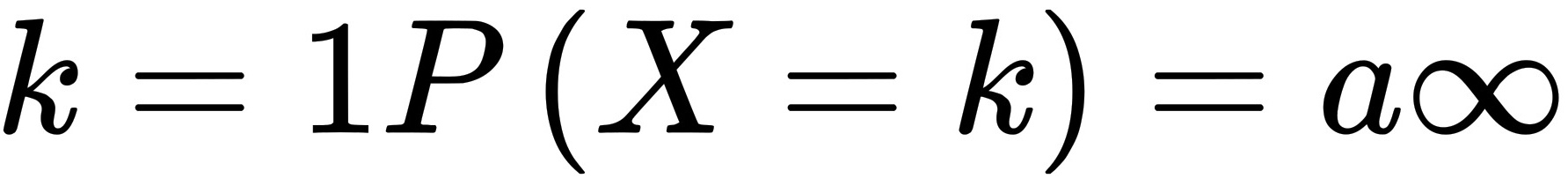

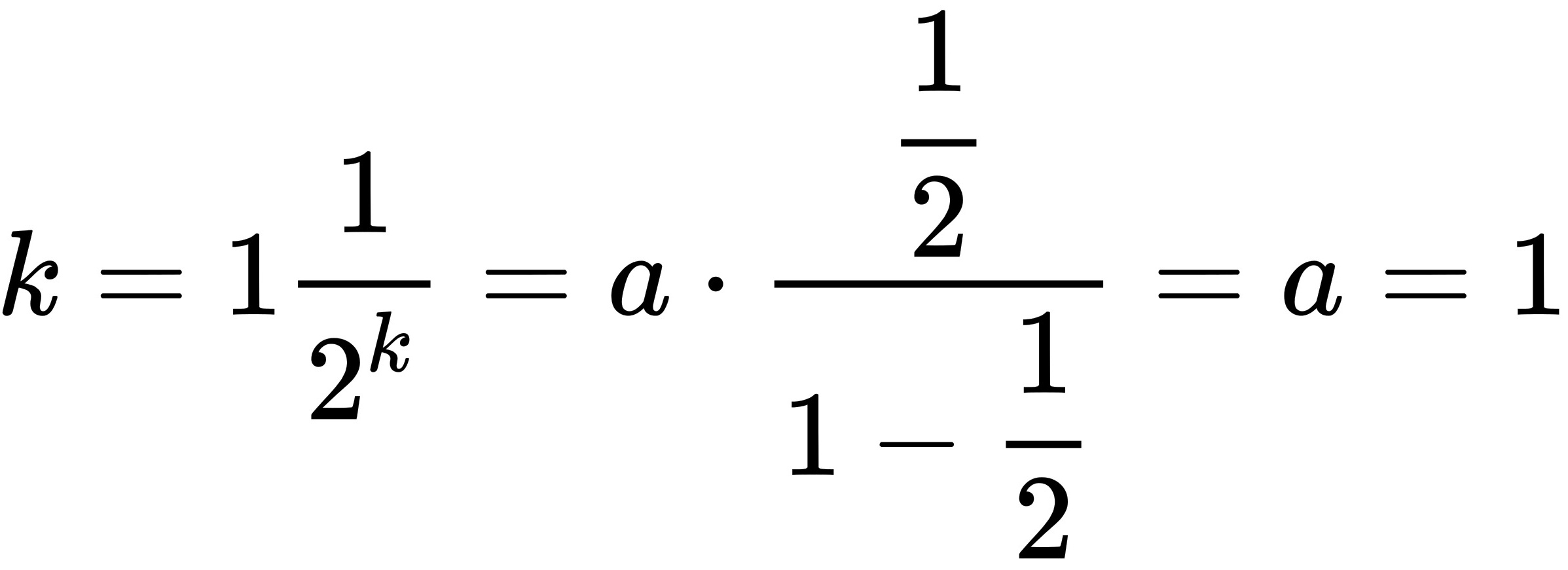 ,即a=1,
,即a=1,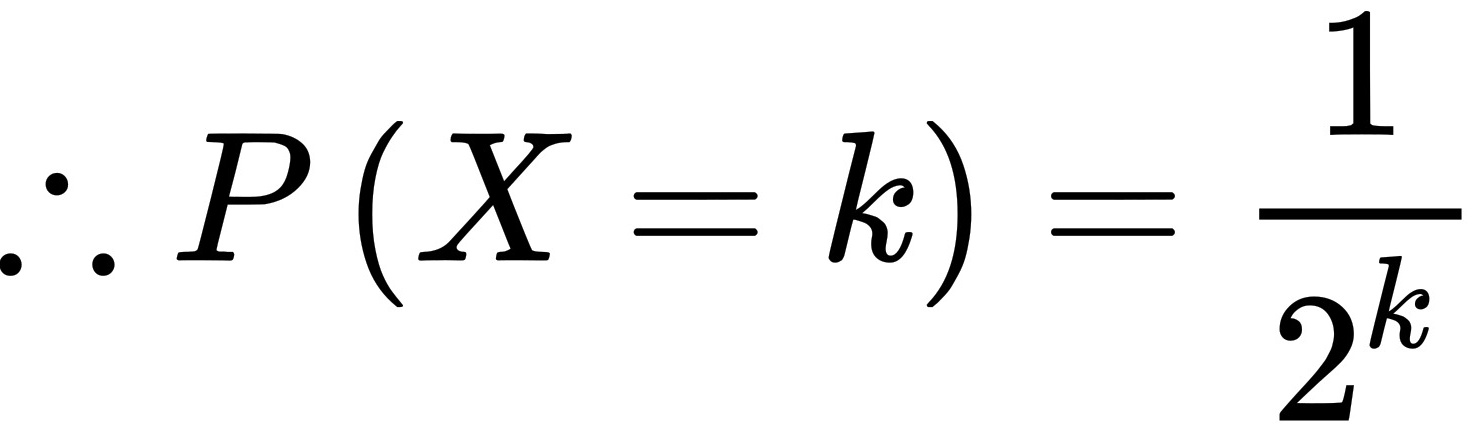 ,k=1,2,
,k=1,2,
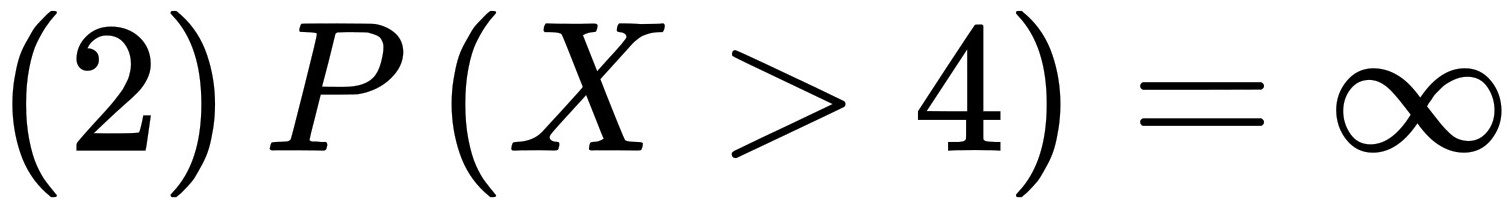

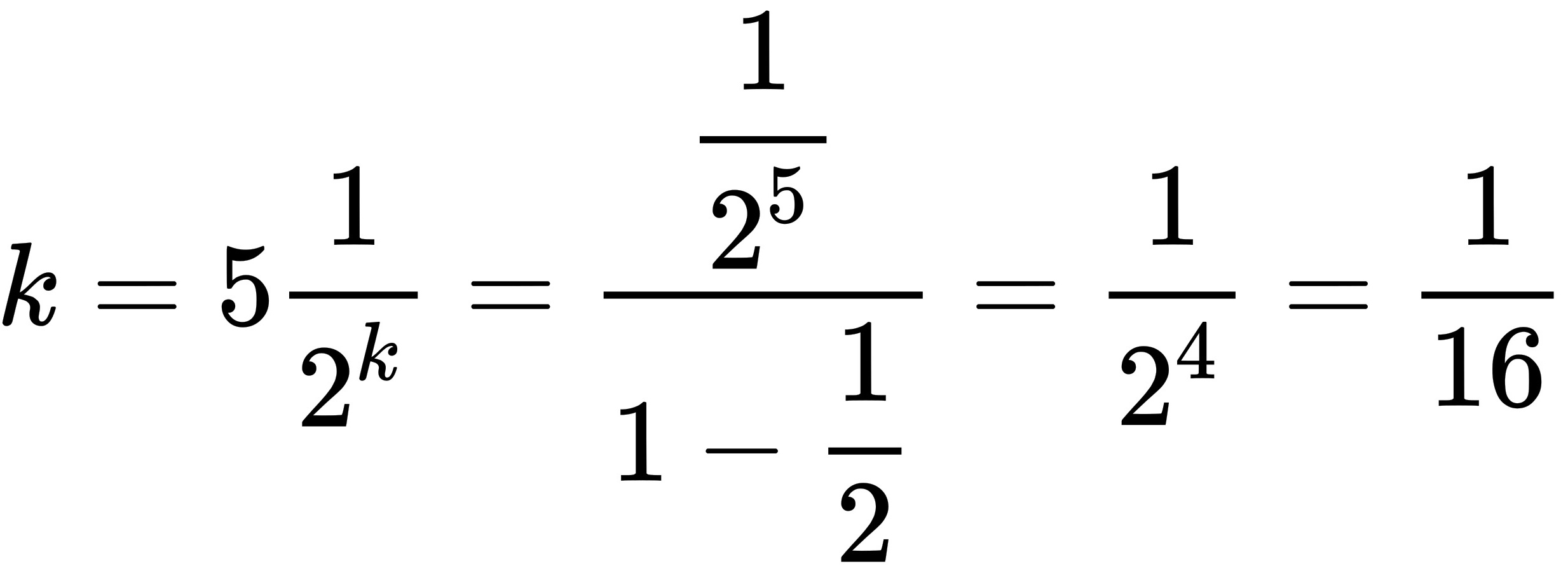
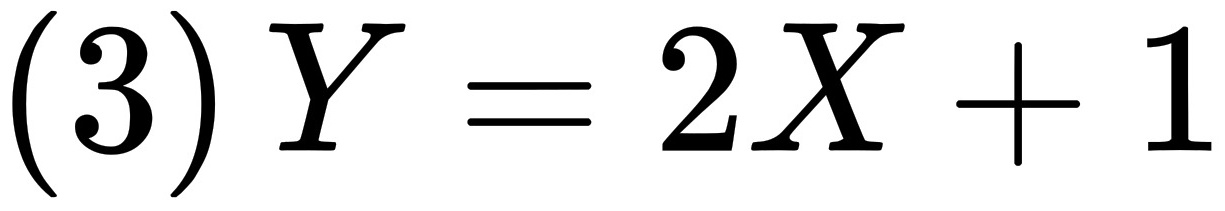 的分布列为
的分布列为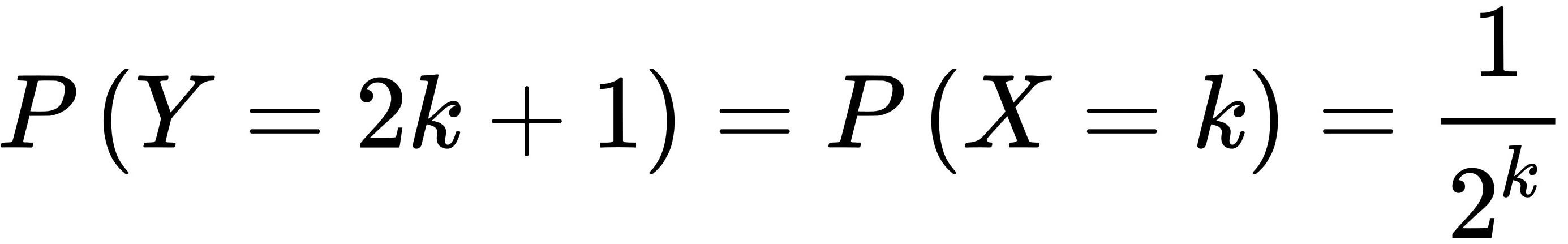 ,k=1,2,
,k=1,2, .
.解析
步骤 1:求参数a
根据概率分布列的性质,所有可能取值的概率之和等于1,即
$$\sum_{k=1}^{\infty} P\{X=k\} = 1$$
代入给定的概率分布列,得到
$$\sum_{k=1}^{\infty} \frac{a}{2^k} = 1$$
这是一个等比数列求和问题,等比数列求和公式为
$$S_n = \frac{a_1(1-q^n)}{1-q}$$
其中,$a_1$是首项,$q$是公比,$n$是项数。对于无穷等比数列,当$|q|<1$时,求和公式为
$$S_{\infty} = \frac{a_1}{1-q}$$
将$a_1 = \frac{a}{2}$,$q = \frac{1}{2}$代入,得到
$$\frac{\frac{a}{2}}{1-\frac{1}{2}} = 1$$
解得$a=1$。
步骤 2:求$P(X>4)$
根据概率分布列,$P(X>4)$表示$X$取值大于4的概率,即
$$P(X>4) = \sum_{k=5}^{\infty} P\{X=k\}$$
代入给定的概率分布列,得到
$$P(X>4) = \sum_{k=5}^{\infty} \frac{1}{2^k}$$
这是一个等比数列求和问题,等比数列求和公式为
$$S_n = \frac{a_1(1-q^n)}{1-q}$$
其中,$a_1$是首项,$q$是公比,$n$是项数。对于无穷等比数列,当$|q|<1$时,求和公式为
$$S_{\infty} = \frac{a_1}{1-q}$$
将$a_1 = \frac{1}{2^5}$,$q = \frac{1}{2}$代入,得到
$$P(X>4) = \frac{\frac{1}{2^5}}{1-\frac{1}{2}} = \frac{1}{2^4} = \frac{1}{16}$$
步骤 3:求$Y=2X+1$的分布列
根据$Y=2X+1$,当$X=k$时,$Y=2k+1$。因此,$Y$的分布列可以表示为
$$P(Y=2k+1) = P(X=k)$$
代入给定的概率分布列,得到
$$P(Y=2k+1) = \frac{1}{2^k}$$
其中,$k=1,2,\cdots$。
根据概率分布列的性质,所有可能取值的概率之和等于1,即
$$\sum_{k=1}^{\infty} P\{X=k\} = 1$$
代入给定的概率分布列,得到
$$\sum_{k=1}^{\infty} \frac{a}{2^k} = 1$$
这是一个等比数列求和问题,等比数列求和公式为
$$S_n = \frac{a_1(1-q^n)}{1-q}$$
其中,$a_1$是首项,$q$是公比,$n$是项数。对于无穷等比数列,当$|q|<1$时,求和公式为
$$S_{\infty} = \frac{a_1}{1-q}$$
将$a_1 = \frac{a}{2}$,$q = \frac{1}{2}$代入,得到
$$\frac{\frac{a}{2}}{1-\frac{1}{2}} = 1$$
解得$a=1$。
步骤 2:求$P(X>4)$
根据概率分布列,$P(X>4)$表示$X$取值大于4的概率,即
$$P(X>4) = \sum_{k=5}^{\infty} P\{X=k\}$$
代入给定的概率分布列,得到
$$P(X>4) = \sum_{k=5}^{\infty} \frac{1}{2^k}$$
这是一个等比数列求和问题,等比数列求和公式为
$$S_n = \frac{a_1(1-q^n)}{1-q}$$
其中,$a_1$是首项,$q$是公比,$n$是项数。对于无穷等比数列,当$|q|<1$时,求和公式为
$$S_{\infty} = \frac{a_1}{1-q}$$
将$a_1 = \frac{1}{2^5}$,$q = \frac{1}{2}$代入,得到
$$P(X>4) = \frac{\frac{1}{2^5}}{1-\frac{1}{2}} = \frac{1}{2^4} = \frac{1}{16}$$
步骤 3:求$Y=2X+1$的分布列
根据$Y=2X+1$,当$X=k$时,$Y=2k+1$。因此,$Y$的分布列可以表示为
$$P(Y=2k+1) = P(X=k)$$
代入给定的概率分布列,得到
$$P(Y=2k+1) = \frac{1}{2^k}$$
其中,$k=1,2,\cdots$。