题目
已知 int xf(x)dx=ln x+C , 求int xf(x)dx=ln x+C .
已知 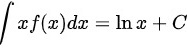 , 求
, 求 .
.
题目解答
答案
给定 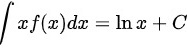 。
。
根据微分的链式法则,我们可以求出:
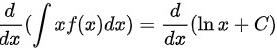
即:
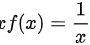
所以,
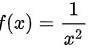
所以,函数 f(x) 的形式为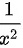 。
。
解析
步骤 1:理解给定的积分表达式
给定的积分表达式为 $\int xf(x)dx=\ln x+C$,其中 $C$ 是积分常数。这意味着 $xf(x)$ 的不定积分是 $\ln x+C$。
步骤 2:求导以找到 $f(x)$
为了找到 $f(x)$,我们需要对等式两边求导。根据微分的链式法则,我们有:
$$\frac{d}{dx}(\int xf(x)dx) = \frac{d}{dx}(\ln x+C)$$
左边的导数是 $xf(x)$,右边的导数是 $\frac{1}{x}$,因为 $C$ 的导数是 0。所以,我们得到:
$$xf(x) = \frac{1}{x}$$
步骤 3:解出 $f(x)$
从上一步得到的等式 $xf(x) = \frac{1}{x}$,我们可以解出 $f(x)$:
$$f(x) = \frac{1}{x^2}$$
给定的积分表达式为 $\int xf(x)dx=\ln x+C$,其中 $C$ 是积分常数。这意味着 $xf(x)$ 的不定积分是 $\ln x+C$。
步骤 2:求导以找到 $f(x)$
为了找到 $f(x)$,我们需要对等式两边求导。根据微分的链式法则,我们有:
$$\frac{d}{dx}(\int xf(x)dx) = \frac{d}{dx}(\ln x+C)$$
左边的导数是 $xf(x)$,右边的导数是 $\frac{1}{x}$,因为 $C$ 的导数是 0。所以,我们得到:
$$xf(x) = \frac{1}{x}$$
步骤 3:解出 $f(x)$
从上一步得到的等式 $xf(x) = \frac{1}{x}$,我们可以解出 $f(x)$:
$$f(x) = \frac{1}{x^2}$$