题目
4.已知两个线性变换:-|||- ) (y)_(1)=(x)_(1)+2(x)_(2)+3(x)_(3) (y)_(2)=-(x)_(1)+3(x)_(2)-(x)_(3) .-|||-;-|||-求(1)从x1,x2,x3到z1,z2的线性变换;(2)从z 1,z2到y1,y2的线性变换.

题目解答
答案
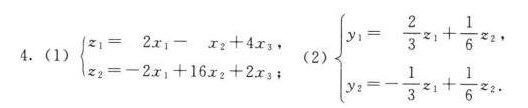
解析
步骤 1:从x1,x2,x3到y1,y2的线性变换
给定的线性变换为:
$$
\left \{ \begin{matrix} {y}_{1}={x}_{1}+2{x}_{2}+3{x}_{3},\\ {y}_{2}=-{x}_{1}+3{x}_{2}-{x}_{3}\end{matrix} \right.
$$
步骤 2:从y1,y2到z1,z2的线性变换
给定的线性变换为:
$$
\left \{ \begin{matrix} {z}_{1}={y}_{1}-{y}_{2},\\ {z}_{2}=2{y}_{1}+4{y}_{2},\end{matrix} \right.
$$
步骤 3:从x1,x2,x3到z1,z2的线性变换
将y1和y2的表达式代入z1和z2的表达式中,得到:
$$
\left \{ \begin{matrix} {z}_{1}=({x}_{1}+2{x}_{2}+3{x}_{3})-(-{x}_{1}+3{x}_{2}-{x}_{3})=2{x}_{1}-{x}_{2}+4{x}_{3},\\ {z}_{2}=2({x}_{1}+2{x}_{2}+3{x}_{3})+4(-{x}_{1}+3{x}_{2}-{x}_{3})=-2{x}_{1}+16{x}_{2}+2{x}_{3}.\end{matrix} \right.
$$
步骤 4:从z1,z2到y1,y2的线性变换
将z1和z2的表达式代入y1和y2的表达式中,得到:
$$
\left \{ \begin{matrix} {y}_{1}=\dfrac {2}{3}{z}_{1}+\dfrac {1}{6}{z}_{2},\\ {y}_{2}=-\dfrac {1}{3}{z}_{1}+\dfrac {1}{6}{z}_{2}.\end{matrix} \right.
$$
给定的线性变换为:
$$
\left \{ \begin{matrix} {y}_{1}={x}_{1}+2{x}_{2}+3{x}_{3},\\ {y}_{2}=-{x}_{1}+3{x}_{2}-{x}_{3}\end{matrix} \right.
$$
步骤 2:从y1,y2到z1,z2的线性变换
给定的线性变换为:
$$
\left \{ \begin{matrix} {z}_{1}={y}_{1}-{y}_{2},\\ {z}_{2}=2{y}_{1}+4{y}_{2},\end{matrix} \right.
$$
步骤 3:从x1,x2,x3到z1,z2的线性变换
将y1和y2的表达式代入z1和z2的表达式中,得到:
$$
\left \{ \begin{matrix} {z}_{1}=({x}_{1}+2{x}_{2}+3{x}_{3})-(-{x}_{1}+3{x}_{2}-{x}_{3})=2{x}_{1}-{x}_{2}+4{x}_{3},\\ {z}_{2}=2({x}_{1}+2{x}_{2}+3{x}_{3})+4(-{x}_{1}+3{x}_{2}-{x}_{3})=-2{x}_{1}+16{x}_{2}+2{x}_{3}.\end{matrix} \right.
$$
步骤 4:从z1,z2到y1,y2的线性变换
将z1和z2的表达式代入y1和y2的表达式中,得到:
$$
\left \{ \begin{matrix} {y}_{1}=\dfrac {2}{3}{z}_{1}+\dfrac {1}{6}{z}_{2},\\ {y}_{2}=-\dfrac {1}{3}{z}_{1}+\dfrac {1}{6}{z}_{2}.\end{matrix} \right.
$$