题目
已知f(x)为可导函数且 '(1)=-2, 则 lim _(harrow 0)dfrac (f(1-h)-f(1-2h))(2h)=
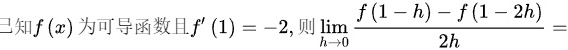
题目解答
答案
首先，我们可以利用泰勒展开公式来近似 ( f(1-h) ) 和 ( f(1-2h) ) 在 ( x = 1 ) 处的值：
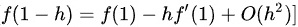
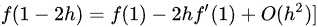
代入 ( f'(1) = -2 ) 得到：
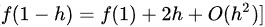
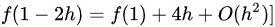
现在，计算差分：
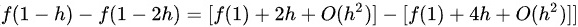
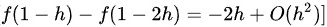
将这个结果代入极限：
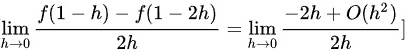
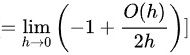
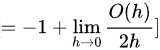
由于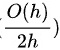 
当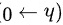 
时趋向于 ( 0 )，因此极限为：
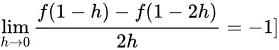
解析
步骤 1：利用泰勒展开公式
利用泰勒展开公式近似 $f(1-h)$ 和 $f(1-2h)$ 在 $x = 1$ 处的值。泰勒展开公式为：
$f(x) = f(a) + f'(a)(x-a) + \frac{f''(a)}{2!}(x-a)^2 + \cdots$
对于 $f(1-h)$ 和 $f(1-2h)$，我们有：
$f(1-h) = f(1) - hf'(1) + O(h^2)$
$f(1-2h) = f(1) - 2hf'(1) + O(h^2)$
步骤 2：代入 $f'(1) = -2$
代入 $f'(1) = -2$，我们得到：
$f(1-h) = f(1) + 2h + O(h^2)$
$f(1-2h) = f(1) + 4h + O(h^2)$
步骤 3：计算差分
计算 $f(1-h) - f(1-2h)$：
$f(1-h) - f(1-2h) = (f(1) + 2h + O(h^2)) - (f(1) + 4h + O(h^2))$
$= -2h + O(h^2)$
步骤 4：代入差分到极限中
代入差分到极限中，我们得到：
$\lim _{h\rightarrow 0}\dfrac {f(1-h)-f(1-2h)}{2h} = \lim _{h\rightarrow 0}\dfrac {-2h + O(h^2)}{2h}$
$= \lim _{h\rightarrow 0}(-1 + \dfrac{O(h^2)}{2h})$
$= -1 + \lim _{h\rightarrow 0}\dfrac{O(h^2)}{2h}$
由于 $\dfrac{O(h^2)}{2h}$ 当 $h \rightarrow 0$ 时趋向于 $0$，因此极限为：
$\lim _{h\rightarrow 0}\dfrac {f(1-h)-f(1-2h)}{2h} = -1$
利用泰勒展开公式近似 $f(1-h)$ 和 $f(1-2h)$ 在 $x = 1$ 处的值。泰勒展开公式为：
$f(x) = f(a) + f'(a)(x-a) + \frac{f''(a)}{2!}(x-a)^2 + \cdots$
对于 $f(1-h)$ 和 $f(1-2h)$，我们有：
$f(1-h) = f(1) - hf'(1) + O(h^2)$
$f(1-2h) = f(1) - 2hf'(1) + O(h^2)$
步骤 2：代入 $f'(1) = -2$
代入 $f'(1) = -2$，我们得到：
$f(1-h) = f(1) + 2h + O(h^2)$
$f(1-2h) = f(1) + 4h + O(h^2)$
步骤 3：计算差分
计算 $f(1-h) - f(1-2h)$：
$f(1-h) - f(1-2h) = (f(1) + 2h + O(h^2)) - (f(1) + 4h + O(h^2))$
$= -2h + O(h^2)$
步骤 4：代入差分到极限中
代入差分到极限中，我们得到：
$\lim _{h\rightarrow 0}\dfrac {f(1-h)-f(1-2h)}{2h} = \lim _{h\rightarrow 0}\dfrac {-2h + O(h^2)}{2h}$
$= \lim _{h\rightarrow 0}(-1 + \dfrac{O(h^2)}{2h})$
$= -1 + \lim _{h\rightarrow 0}\dfrac{O(h^2)}{2h}$
由于 $\dfrac{O(h^2)}{2h}$ 当 $h \rightarrow 0$ 时趋向于 $0$，因此极限为：
$\lim _{h\rightarrow 0}\dfrac {f(1-h)-f(1-2h)}{2h} = -1$