题目
(int )_(1)^edfrac (ln x)(x)dx.
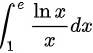 .
.
题目解答
答案
我们知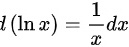 ,故定积分
,故定积分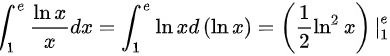
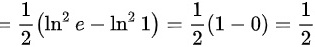 .
.
解析
步骤 1:确定积分变量和积分区间
题目要求计算定积分 ${\int }_{1}^{e}\dfrac {\ln x}{x}dx$,其中积分变量为 $x$,积分区间为 $[1, e]$。
步骤 2:使用换元法
令 $u = \ln x$,则 $du = \dfrac {1}{x}dx$。当 $x = 1$ 时,$u = \ln 1 = 0$;当 $x = e$ 时,$u = \ln e = 1$。因此,原积分可以写为 ${\int }_{0}^{1}u du$。
步骤 3:计算积分
${\int }_{0}^{1}u du = \dfrac {1}{2}u^2{\int }_{0}^{1} = \dfrac {1}{2}(1^2 - 0^2) = \dfrac {1}{2}$。
题目要求计算定积分 ${\int }_{1}^{e}\dfrac {\ln x}{x}dx$,其中积分变量为 $x$,积分区间为 $[1, e]$。
步骤 2:使用换元法
令 $u = \ln x$,则 $du = \dfrac {1}{x}dx$。当 $x = 1$ 时,$u = \ln 1 = 0$;当 $x = e$ 时,$u = \ln e = 1$。因此,原积分可以写为 ${\int }_{0}^{1}u du$。
步骤 3:计算积分
${\int }_{0}^{1}u du = \dfrac {1}{2}u^2{\int }_{0}^{1} = \dfrac {1}{2}(1^2 - 0^2) = \dfrac {1}{2}$。