题目
求微分方程 (x-1)dfrac (dy)(dx)=((x-1))^2+y的通解。
求微分方程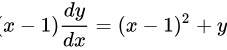 
的通解。
题目解答
答案
由题意微分方程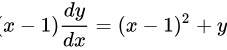
对方程两边同时除以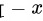
，然后移项整理得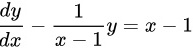
该方程为一阶线性微分方程
则方程通解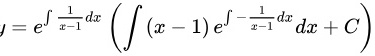
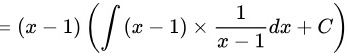
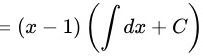
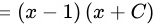
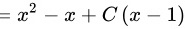，C为任意常数
故答案为：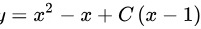
解析
步骤 1：整理方程
将方程 $(x-1)\dfrac {dy}{dx}={(x-1)}^{2}+y$ 整理为标准形式，即 $\dfrac {dy}{dx}-\dfrac {1}{x-1}y=x-1$。这是通过将方程两边同时除以$(x-1)$，然后移项得到的。
步骤 2：识别方程类型
方程 $\dfrac {dy}{dx}-\dfrac {1}{x-1}y=x-1$ 是一阶线性微分方程，其标准形式为 $\dfrac {dy}{dx}+P(x)y=Q(x)$，其中$P(x)=-\dfrac {1}{x-1}$，$Q(x)=x-1$。
步骤 3：求解通解
一阶线性微分方程的通解公式为 $y=e^{-\int P(x)dx}[\int Q(x)e^{\int P(x)dx}dx+C]$。将$P(x)$和$Q(x)$代入，得到$y=e^{\int \dfrac {1}{x-1}dx}[\int (x-1)e^{-\int \dfrac {1}{x-1}dx}dx+C]$。计算积分，得到$y=(x-1)[\int (x-1)\dfrac {1}{x-1}dx+C]$。进一步简化，得到$y=(x-1)[\int dx+C]$。最后，得到$y=(x-1)(x+C)$。
将方程 $(x-1)\dfrac {dy}{dx}={(x-1)}^{2}+y$ 整理为标准形式，即 $\dfrac {dy}{dx}-\dfrac {1}{x-1}y=x-1$。这是通过将方程两边同时除以$(x-1)$，然后移项得到的。
步骤 2：识别方程类型
方程 $\dfrac {dy}{dx}-\dfrac {1}{x-1}y=x-1$ 是一阶线性微分方程，其标准形式为 $\dfrac {dy}{dx}+P(x)y=Q(x)$，其中$P(x)=-\dfrac {1}{x-1}$，$Q(x)=x-1$。
步骤 3：求解通解
一阶线性微分方程的通解公式为 $y=e^{-\int P(x)dx}[\int Q(x)e^{\int P(x)dx}dx+C]$。将$P(x)$和$Q(x)$代入，得到$y=e^{\int \dfrac {1}{x-1}dx}[\int (x-1)e^{-\int \dfrac {1}{x-1}dx}dx+C]$。计算积分，得到$y=(x-1)[\int (x-1)\dfrac {1}{x-1}dx+C]$。进一步简化，得到$y=(x-1)[\int dx+C]$。最后，得到$y=(x-1)(x+C)$。