题目
已知等差数列 12 , 8 , 4 , 0...... 求它的通项公式u2 和前 10 项 的和u2
已知等差数列 12 , 8 , 4 , 0...... 求它的通项公式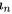 和前 10 项 的和
和前 10 项 的和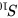
题目解答
答案
解:
由题意可得,d=-4,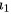 =12
=12
∴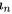 =
= 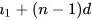 =16-4n
=16-4n
∴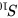 =
=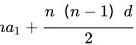 =-60
=-60
解析
考查要点:本题主要考查等差数列的通项公式和前n项和的计算,需要掌握公差的确定方法以及求和公式的应用。
解题核心思路:
- 确定首项和公差:通过观察数列前几项,直接得出首项$a_1$,再用后项减前项得到公差$d$。
- 通项公式推导:利用公式$a_n = a_1 + (n-1)d$,代入已知值并化简。
- 前n项和计算:选择公式$S_n = \frac{n}{2}[2a_1 + (n-1)d]$或$S_n = \frac{n(a_1 + a_n)}{2}$,代入数值计算。
破题关键点:
- 公差的正负:注意公差为负数时,通项公式中的符号处理。
- 公式代入的准确性:确保代入求和公式时各项数值正确,避免计算错误。
通项公式推导
- 确定首项和公差:
- 首项$a_1 = 12$。
- 公差$d = 8 - 12 = -4$。
- 代入通项公式:
$a_n = a_1 + (n-1)d = 12 + (n-1)(-4)$ - 化简表达式:
$a_n = 12 - 4(n-1) = 12 - 4n + 4 = 16 - 4n$
前10项和计算
- 选择求和公式:
$S_{10} = \frac{10}{2} \left[ 2 \cdot 12 + (10-1) \cdot (-4) \right]$ - 分步计算:
- 计算括号内部分:
$2 \cdot 12 = 24, \quad 9 \cdot (-4) = -36, \quad 24 + (-36) = -12$ - 代入公式:
$S_{10} = 5 \cdot (-12) = -60$
- 计算括号内部分: