题目
8.设二维随机变量(X,Y)的联合概率密度为-|||-f(x,y)= ) 6(1-y),0lt xlt ylt 1 0

题目解答
答案
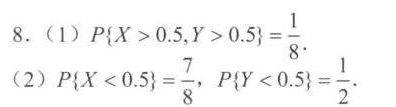
解析
步骤 1:计算 $P\{ X\gt 0.5,Y\gt 0.5\}$
根据联合概率密度函数 $f(x,y)$,我们首先需要确定积分的范围。由于 $0\lt x\lt y\lt 1$,且 $x\gt 0.5$ 和 $y\gt 0.5$,因此积分范围为 $0.5\lt x\lt y\lt 1$。因此,$P\{ X\gt 0.5,Y\gt 0.5\}$ 可以表示为:
$$
P\{ X\gt 0.5,Y\gt 0.5\} = \int_{0.5}^{1} \int_{0.5}^{y} 6(1-y) \, dx \, dy
$$
步骤 2:计算 $P\{ X\lt 0.5\}$
$P\{ X\lt 0.5\}$ 可以表示为:
$$
P\{ X\lt 0.5\} = \int_{0}^{0.5} \int_{x}^{1} 6(1-y) \, dy \, dx
$$
步骤 3:计算 $P\{ Y\lt 0.5\}$
$P\{ Y\lt 0.5\}$ 可以表示为:
$$
P\{ Y\lt 0.5\} = \int_{0}^{0.5} \int_{0}^{y} 6(1-y) \, dx \, dy
$$
根据联合概率密度函数 $f(x,y)$,我们首先需要确定积分的范围。由于 $0\lt x\lt y\lt 1$,且 $x\gt 0.5$ 和 $y\gt 0.5$,因此积分范围为 $0.5\lt x\lt y\lt 1$。因此,$P\{ X\gt 0.5,Y\gt 0.5\}$ 可以表示为:
$$
P\{ X\gt 0.5,Y\gt 0.5\} = \int_{0.5}^{1} \int_{0.5}^{y} 6(1-y) \, dx \, dy
$$
步骤 2:计算 $P\{ X\lt 0.5\}$
$P\{ X\lt 0.5\}$ 可以表示为:
$$
P\{ X\lt 0.5\} = \int_{0}^{0.5} \int_{x}^{1} 6(1-y) \, dy \, dx
$$
步骤 3:计算 $P\{ Y\lt 0.5\}$
$P\{ Y\lt 0.5\}$ 可以表示为:
$$
P\{ Y\lt 0.5\} = \int_{0}^{0.5} \int_{0}^{y} 6(1-y) \, dx \, dy
$$