题目
设长方体的长、宽、高分别为c,y,z,求表面积为6时体积最大的长方体的体积.
设长方体的长、宽、高分别为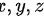 ,求表面积为6时体积最大的长方体的体积.
,求表面积为6时体积最大的长方体的体积.
题目解答
答案
长方体表面积为6,则有关系式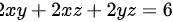 ,即
,即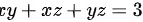 ,设长方体的体积为
,设长方体的体积为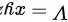 ,利用拉格朗日乘数法,令
,利用拉格朗日乘数法,令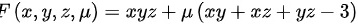 ,则有
,则有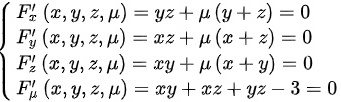 ,得到
,得到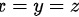 ,代入
,代入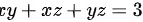 中,可知
中,可知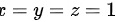 ,故最大的长方体的体积为
,故最大的长方体的体积为 .
.
解析
步骤 1:建立体积和表面积的关系
长方体的体积$V=xyz$,表面积$S=2(xy+xz+yz)$。题目中给出表面积$S=6$,即$2(xy+xz+yz)=6$,简化得到$xy+xz+yz=3$。
步骤 2:利用拉格朗日乘数法求解
为了求解体积$V=xyz$的最大值,我们引入拉格朗日乘数法。设$L(x,y,z,\lambda)=xyz+\lambda(xy+xz+yz-3)$,其中$\lambda$是拉格朗日乘数。对$L$分别对$x,y,z$求偏导数并令其等于0,得到方程组:
$$
\left \{ \begin{matrix}
yz+\lambda(y+z)=0\\
xz+\lambda(x+z)=0\\
xy+\lambda(x+y)=0\\
xy+xz+yz=3
\end{matrix} \right.
$$
步骤 3:求解方程组
从方程组中,我们可以观察到$x,y,z$在方程中地位相同,因此可以推断出$x=y=z$。将$x=y=z$代入$xy+xz+yz=3$中,得到$3x^2=3$,解得$x=1$。因此,$x=y=z=1$。
步骤 4:计算最大体积
将$x=y=z=1$代入体积公式$V=xyz$中,得到$V=1\cdot 1\cdot 1=1$。
长方体的体积$V=xyz$,表面积$S=2(xy+xz+yz)$。题目中给出表面积$S=6$,即$2(xy+xz+yz)=6$,简化得到$xy+xz+yz=3$。
步骤 2:利用拉格朗日乘数法求解
为了求解体积$V=xyz$的最大值,我们引入拉格朗日乘数法。设$L(x,y,z,\lambda)=xyz+\lambda(xy+xz+yz-3)$,其中$\lambda$是拉格朗日乘数。对$L$分别对$x,y,z$求偏导数并令其等于0,得到方程组:
$$
\left \{ \begin{matrix}
yz+\lambda(y+z)=0\\
xz+\lambda(x+z)=0\\
xy+\lambda(x+y)=0\\
xy+xz+yz=3
\end{matrix} \right.
$$
步骤 3:求解方程组
从方程组中,我们可以观察到$x,y,z$在方程中地位相同,因此可以推断出$x=y=z$。将$x=y=z$代入$xy+xz+yz=3$中,得到$3x^2=3$,解得$x=1$。因此,$x=y=z=1$。
步骤 4:计算最大体积
将$x=y=z=1$代入体积公式$V=xyz$中,得到$V=1\cdot 1\cdot 1=1$。