题目
(2)已知函数f(x)= ) 2(x-1),xlt 1 ln x,xgeqslant 1 .
(2)已知函数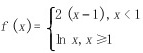 ,则
,则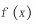 的一个原函数是( )
的一个原函数是( )
A、
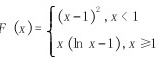
B、
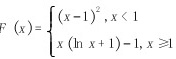
C、
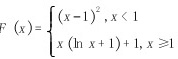
D、
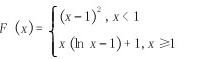
题目解答
答案
D
解析
考查要点:本题主要考查分段函数的原函数求解,需满足两个条件:
- 分段区间内导数正确:每个分段区间的原函数求导后应等于原函数在对应区间的表达式;
- 分段点连续性:原函数在分段点(此处为$x=1$)必须连续,否则导数可能不存在。
解题核心思路:
- 分段积分:分别对$x<1$和$x \geq 1$的区间求原函数;
- 调整常数项:确保原函数在$x=1$处连续,确定积分常数;
- 验证选项:对每个选项求导并检查连续性,排除错误选项。
步骤1:求$x<1$时的原函数
当$x<1$时,$f(x)=2(x-1)$,积分得:
$\int 2(x-1) \, dx = (x-1)^2 + C_1$
所有选项在$x<1$时均为$(x-1)^2$,故无需区分,重点分析$x \geq 1$部分。
步骤2:求$x \geq 1$时的原函数
当$x \geq 1$时,$f(x)=\ln x$,积分得:
$\int \ln x \, dx = x(\ln x - 1) + C_2$
需通过连续性条件确定$C_2$:
- 当$x \to 1^-$时,原函数值为$(1-1)^2 = 0$;
- 当$x=1$时,$x(\ln 1 - 1) + C_2 = -1 + C_2$;
- 连续性要求$-1 + C_2 = 0 \implies C_2 = 1$,故$x \geq 1$的原函数为:
$x(\ln x - 1) + 1$
步骤3:验证选项
- 选项D:$x \geq 1$时为$x(\ln x - 1) + 1$,导数为$\ln x$,且在$x=1$处连续;
- 其他选项:导数错误或不连续(如选项B导数为$\ln x + 2$,选项A在$x=1$处不连续)。