题目
(5) int (tan )^10xcdot (sec )^2xdx;
题目解答
答案
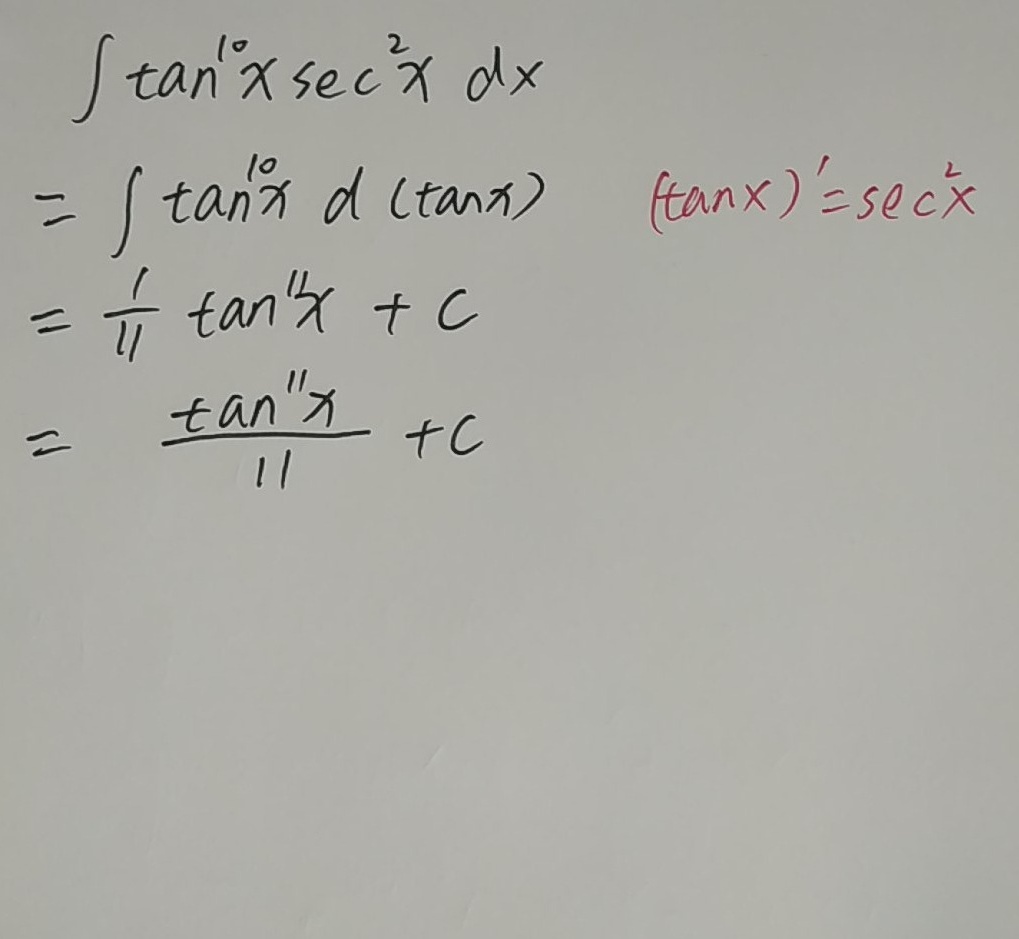
解析
步骤 1:识别积分形式
观察积分 $\int {\tan }^{10}x\cdot {\sec }^{2}xdx$,注意到 ${\sec }^{2}x$ 是 $\tan x$ 的导数,即 $(\tan x)' = {\sec }^{2}x$。这提示我们可以使用换元法,将 $\tan x$ 作为新的变量。
步骤 2:换元
设 $u = \tan x$,则 $du = {\sec }^{2}x dx$。将原积分中的 $\tan x$ 和 ${\sec }^{2}x dx$ 替换为 $u$ 和 $du$,得到 $\int u^{10} du$。
步骤 3:计算积分
计算 $\int u^{10} du$,根据幂函数的积分公式 $\int u^n du = \frac{u^{n+1}}{n+1} + C$,得到 $\int u^{10} du = \frac{u^{11}}{11} + C$。
步骤 4:回代
将 $u = \tan x$ 回代到积分结果中,得到 $\frac{\tan^{11} x}{11} + C$。
观察积分 $\int {\tan }^{10}x\cdot {\sec }^{2}xdx$,注意到 ${\sec }^{2}x$ 是 $\tan x$ 的导数,即 $(\tan x)' = {\sec }^{2}x$。这提示我们可以使用换元法,将 $\tan x$ 作为新的变量。
步骤 2:换元
设 $u = \tan x$,则 $du = {\sec }^{2}x dx$。将原积分中的 $\tan x$ 和 ${\sec }^{2}x dx$ 替换为 $u$ 和 $du$,得到 $\int u^{10} du$。
步骤 3:计算积分
计算 $\int u^{10} du$,根据幂函数的积分公式 $\int u^n du = \frac{u^{n+1}}{n+1} + C$,得到 $\int u^{10} du = \frac{u^{11}}{11} + C$。
步骤 4:回代
将 $u = \tan x$ 回代到积分结果中,得到 $\frac{\tan^{11} x}{11} + C$。