题目
(int )_(a)^bf'(2x)dx=_____.
_____.
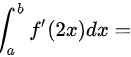题目解答
答案
已知定积分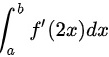
，我们令
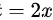，则有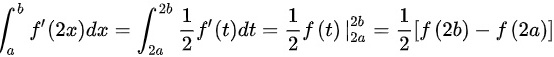
故答案为：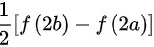
解析
步骤 1：换元
令 $t = 2x$，则 $dt = 2dx$，即 $dx = \frac{1}{2}dt$。
步骤 2：积分区间变换
当 $x = a$ 时，$t = 2a$；当 $x = b$ 时，$t = 2b$。因此，积分区间从 $[a, b]$ 变换为 $[2a, 2b]$。
步骤 3：代入并计算
将换元后的表达式代入原积分，得到 ${\int }_{a}^{b}f'(2x)dx = {\int }_{2a}^{2b}f'(t) \cdot \frac{1}{2}dt = \frac{1}{2}{\int }_{2a}^{2b}f'(t)dt$。
步骤 4：计算定积分
根据定积分的性质，${\int }_{2a}^{2b}f'(t)dt = f(t)|_{2a}^{2b} = f(2b) - f(2a)$。
步骤 5：最终结果
将步骤 4 的结果代入步骤 3 的表达式，得到 ${\int }_{a}^{b}f'(2x)dx = \frac{1}{2}[f(2b) - f(2a)]$。
令 $t = 2x$，则 $dt = 2dx$，即 $dx = \frac{1}{2}dt$。
步骤 2：积分区间变换
当 $x = a$ 时，$t = 2a$；当 $x = b$ 时，$t = 2b$。因此，积分区间从 $[a, b]$ 变换为 $[2a, 2b]$。
步骤 3：代入并计算
将换元后的表达式代入原积分，得到 ${\int }_{a}^{b}f'(2x)dx = {\int }_{2a}^{2b}f'(t) \cdot \frac{1}{2}dt = \frac{1}{2}{\int }_{2a}^{2b}f'(t)dt$。
步骤 4：计算定积分
根据定积分的性质，${\int }_{2a}^{2b}f'(t)dt = f(t)|_{2a}^{2b} = f(2b) - f(2a)$。
步骤 5：最终结果
将步骤 4 的结果代入步骤 3 的表达式，得到 ${\int }_{a}^{b}f'(2x)dx = \frac{1}{2}[f(2b) - f(2a)]$。