题目
[题目]函数 y=y(x) 由方程 sin ((x)^2+(y)^2)+(e)^x-x(y)^2=0 所-|||-确定,则 dfrac (dy)(dx)= __

题目解答
答案
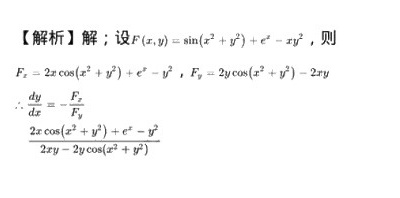
解析
步骤 1:定义函数
设 $F(x,y)=\sin ({x}^{2}+{y}^{2})+{e}^{x}-x{y}^{2}$。
步骤 2:计算偏导数
计算 $F(x,y)$ 对 $x$ 的偏导数 ${F}_{x}$ 和对 $y$ 的偏导数 ${F}_{y}$。
${F}_{x}=2x\cos ({x}^{2}+{y}^{2})+{e}^{x}-{y}^{2}$,
${F}_{y}=2y\cos ({x}^{2}+{y}^{2})-2xy$。
步骤 3:应用隐函数求导公式
根据隐函数求导公式,$\dfrac {dy}{dx}=-\dfrac {{F}_{x}}{{F}_{y}}$。
设 $F(x,y)=\sin ({x}^{2}+{y}^{2})+{e}^{x}-x{y}^{2}$。
步骤 2:计算偏导数
计算 $F(x,y)$ 对 $x$ 的偏导数 ${F}_{x}$ 和对 $y$ 的偏导数 ${F}_{y}$。
${F}_{x}=2x\cos ({x}^{2}+{y}^{2})+{e}^{x}-{y}^{2}$,
${F}_{y}=2y\cos ({x}^{2}+{y}^{2})-2xy$。
步骤 3:应用隐函数求导公式
根据隐函数求导公式,$\dfrac {dy}{dx}=-\dfrac {{F}_{x}}{{F}_{y}}$。