题目
6.已知 f(x )的一个原函数为 ^-x ,则 int xf'(x)dx=( ) ()-|||-A . (e)^-x+(e)^-x+C B. (e)^-x-e

题目解答
答案
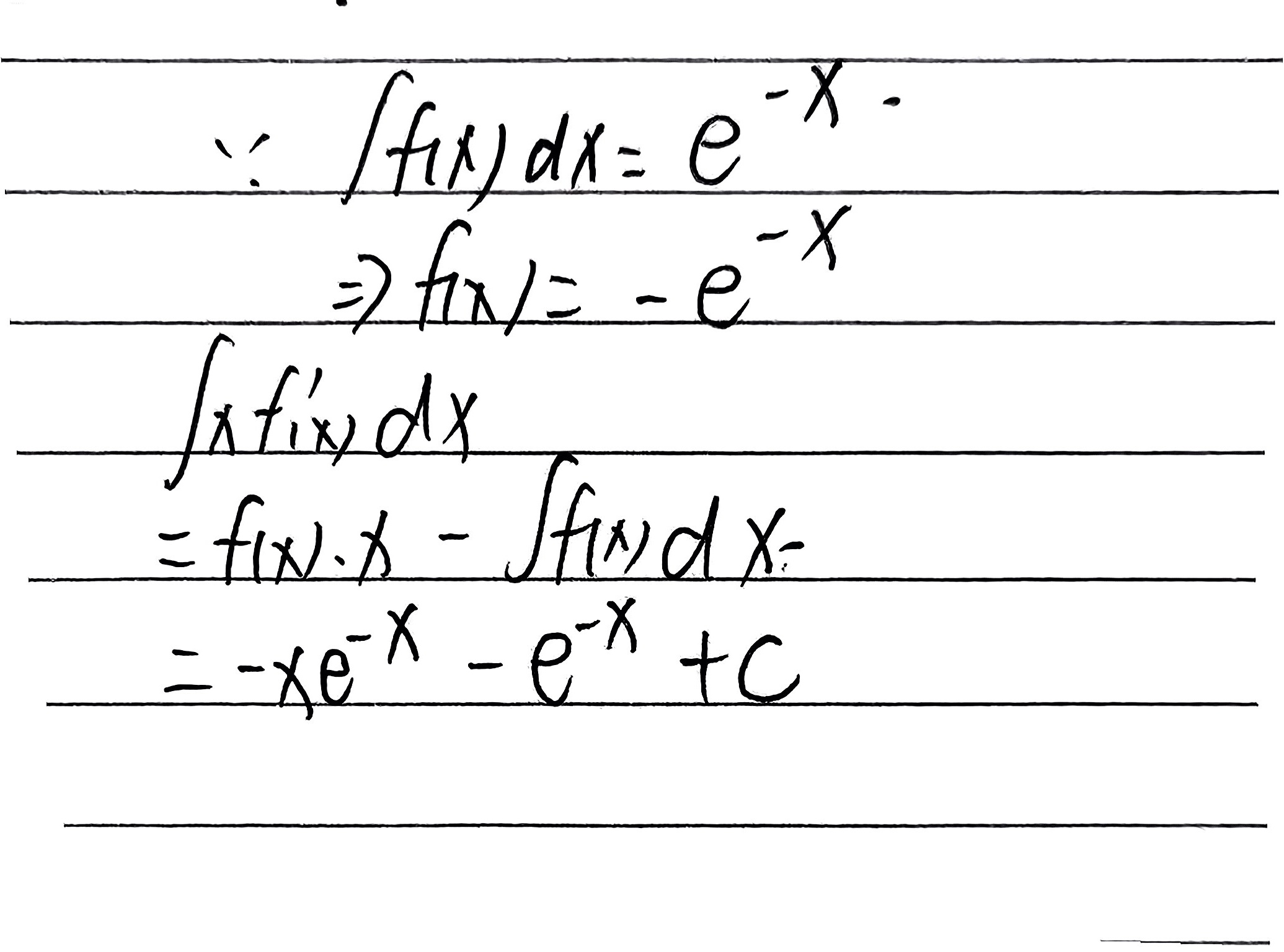
解析
步骤 1:确定 f(x) 的表达式
已知 f(x) 的一个原函数为 ${e}^{-x}$,即 $\int f(x)dx = {e}^{-x} + C$。因此,f(x) 是 ${e}^{-x}$ 的导数,即 $f(x) = -{e}^{-x}$。
步骤 2:应用分部积分法
根据分部积分法,$\int u dv = uv - \int v du$。这里,我们设 $u = x$,$dv = f'(x)dx$,则 $du = dx$,$v = f(x)$。因此,$\int xf'(x)dx = x f(x) - \int f(x)dx$。
步骤 3:代入 f(x) 的表达式
将 $f(x) = -{e}^{-x}$ 代入上式,得到 $\int xf'(x)dx = x(-{e}^{-x}) - \int (-{e}^{-x})dx$。进一步计算,得到 $\int xf'(x)dx = -x{e}^{-x} + {e}^{-x} + C$。
已知 f(x) 的一个原函数为 ${e}^{-x}$,即 $\int f(x)dx = {e}^{-x} + C$。因此,f(x) 是 ${e}^{-x}$ 的导数,即 $f(x) = -{e}^{-x}$。
步骤 2:应用分部积分法
根据分部积分法,$\int u dv = uv - \int v du$。这里,我们设 $u = x$,$dv = f'(x)dx$,则 $du = dx$,$v = f(x)$。因此,$\int xf'(x)dx = x f(x) - \int f(x)dx$。
步骤 3:代入 f(x) 的表达式
将 $f(x) = -{e}^{-x}$ 代入上式,得到 $\int xf'(x)dx = x(-{e}^{-x}) - \int (-{e}^{-x})dx$。进一步计算,得到 $\int xf'(x)dx = -x{e}^{-x} + {e}^{-x} + C$。