题目
2.设一平面垂直于平面z=0,并通过从点(1,-1,1)到直线y - .z +1=0-|||-x:=0的垂线,求此平面的方程.
2.设一平面垂直于平面z=0,并通过从点(1,-1,1)到直线
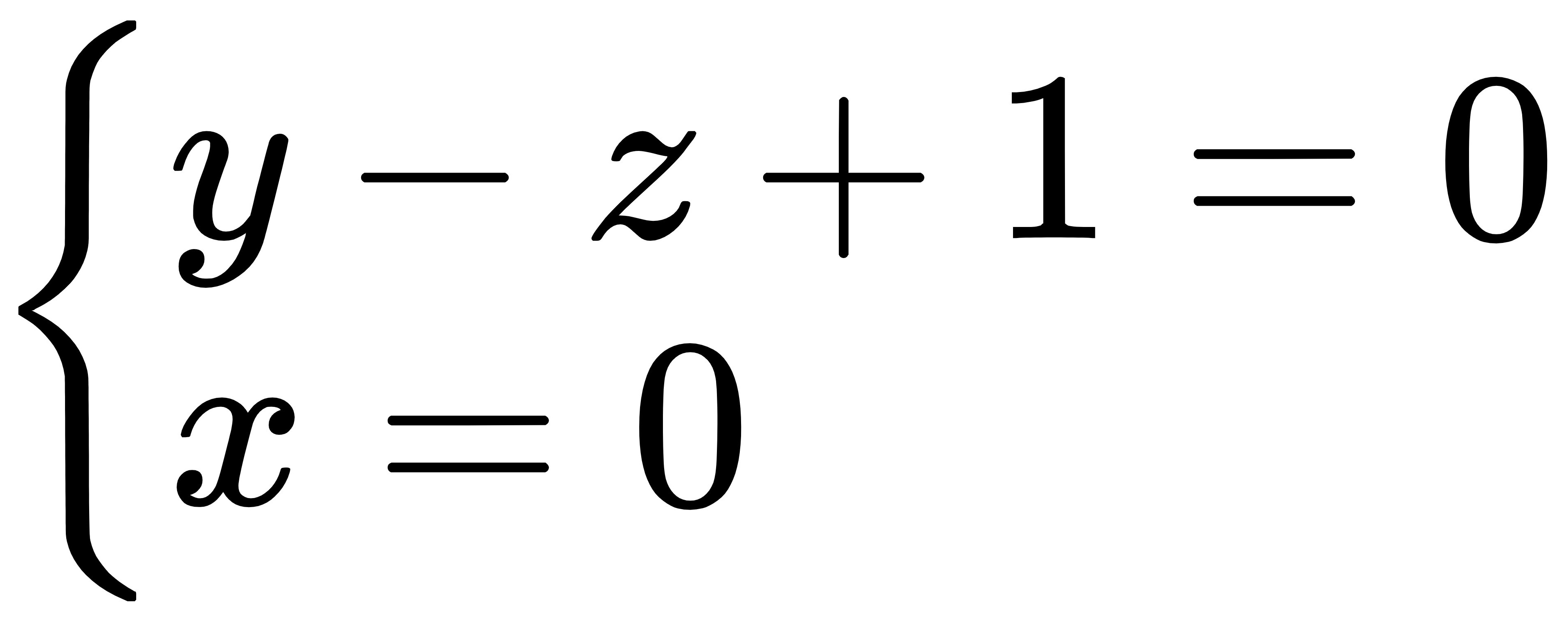
的垂线,求此平面的方程.
题目解答
答案
∴

解析
步骤 1:确定直线的方向向量
直线 $\left \{ \begin{matrix} y-z+1=0\\ x=0\end{matrix} \right.$ 的方向向量可以通过求解两个平面的法向量的叉积得到。平面 $y-z+1=0$ 的法向量为 $\vec{n_1}=(0,1,-1)$,平面 $x=0$ 的法向量为 $\vec{n_2}=(1,0,0)$。因此,直线的方向向量 $\vec{s}=\vec{n_1} \times \vec{n_2}=(0,-1,-1)$。
步骤 2:确定垂足
过点 $(1,-1,1)$ 且以 $\vec{s}=(0,-1,-1)$ 为法向量的平面方程为 $-1\cdot (y+1)-(z-1)=0$,即 $y+z=0$。联立直线方程 $\left \{ \begin{matrix} y-z+1=0\\ x=0\\ y+z=0\end{matrix} \right.$,解得垂足为 $(0,-\dfrac {1}{2},\dfrac {1}{2})$。
步骤 3:确定所求平面的方程
所求平面垂直于平面 $z=0$,设平面方程为 $Ax+By+D=0$。平面过点 $(1,-1,1)$ 及垂足 $(0,-\dfrac {1}{2},\dfrac {1}{2})$,代入方程得 $\left \{ \begin{matrix} A-B+D=0\\ -\dfrac {1}{2}B+D=0\end{matrix} \right.$,解得 $B=2D$,$A=D$。因此,所求平面方程为 $Dx+2Dy+D=0$,即 $x+2y+1=0$。
直线 $\left \{ \begin{matrix} y-z+1=0\\ x=0\end{matrix} \right.$ 的方向向量可以通过求解两个平面的法向量的叉积得到。平面 $y-z+1=0$ 的法向量为 $\vec{n_1}=(0,1,-1)$,平面 $x=0$ 的法向量为 $\vec{n_2}=(1,0,0)$。因此,直线的方向向量 $\vec{s}=\vec{n_1} \times \vec{n_2}=(0,-1,-1)$。
步骤 2:确定垂足
过点 $(1,-1,1)$ 且以 $\vec{s}=(0,-1,-1)$ 为法向量的平面方程为 $-1\cdot (y+1)-(z-1)=0$,即 $y+z=0$。联立直线方程 $\left \{ \begin{matrix} y-z+1=0\\ x=0\\ y+z=0\end{matrix} \right.$,解得垂足为 $(0,-\dfrac {1}{2},\dfrac {1}{2})$。
步骤 3:确定所求平面的方程
所求平面垂直于平面 $z=0$,设平面方程为 $Ax+By+D=0$。平面过点 $(1,-1,1)$ 及垂足 $(0,-\dfrac {1}{2},\dfrac {1}{2})$,代入方程得 $\left \{ \begin{matrix} A-B+D=0\\ -\dfrac {1}{2}B+D=0\end{matrix} \right.$,解得 $B=2D$,$A=D$。因此,所求平面方程为 $Dx+2Dy+D=0$,即 $x+2y+1=0$。