题目
设 (x)=(e)^-x, 则 int dfrac (f'(ln x))(x)dx= .(x)=(e)^-x, 则 int dfrac (f'(ln x))(x)dx= .
设 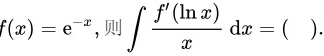
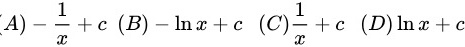
题目解答
答案
我们先对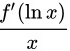 进行一些简单的变形:
进行一些简单的变形:
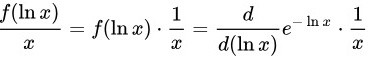
由链式法则,有
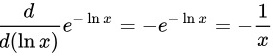
代入上面的式子,得到:
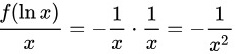
因此,原式可以化简为:
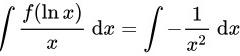
对积分进行求解,得到:
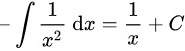
解析
考查要点:本题主要考查复合函数的导数计算及不定积分的基本方法。关键在于正确求出$f'(\ln x)$,并将其代入积分表达式进行化简。
解题思路:
- 求导:先对$f(x)=e^{-x}$求导,得到$f'(x)=-e^{-x}$;
- 变量替换:将$\ln x$代入$f'(x)$中,得到$f'(\ln x)=-e^{-\ln x}=-\frac{1}{x}$;
- 化简积分式:将$f'(\ln x)/x$代入积分表达式,转化为$\int -\frac{1}{x^2}dx$;
- 积分计算:直接应用幂函数积分公式求解。
破题关键:正确应用链式法则求导,并注意变量替换后的化简。
步骤1:求$f'(x)$
已知$f(x)=e^{-x}$,则其导数为:
$f'(x) = \frac{d}{dx} e^{-x} = -e^{-x}$
步骤2:计算$f'(\ln x)$
将$x$替换为$\ln x$,得:
$f'(\ln x) = -e^{-\ln x} = -\frac{1}{x}$
步骤3:代入积分表达式
原积分式为:
$\int \frac{f'(\ln x)}{x} dx = \int \frac{-\frac{1}{x}}{x} dx = \int -\frac{1}{x^2} dx$
步骤4:计算积分
利用幂函数积分公式$\int x^n dx = \frac{x^{n+1}}{n+1} + C$($n \neq -1$):
$\int -\frac{1}{x^2} dx = -\int x^{-2} dx = -\left( \frac{x^{-1}}{-1} \right) + C = \frac{1}{x} + C$