题目
[题目]设函数g (x)可微, (x)=(e)^1+g(x) ,h`(1)=1,-|||-'(1)=2, 则g(1)等于 ()-|||-A. ln 3-1-|||-B. -ln 3-1-|||-C. -ln 2-1-|||-D. ln 2-1

题目解答
答案
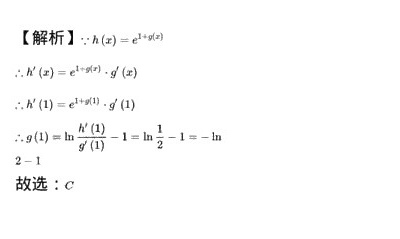
解析
考查要点:本题主要考查复合函数的导数计算及对数方程的求解能力。
解题思路:
- 利用链式法则求导:对函数$h(x)=e^{1+g(x)}$求导,得到$h'(x)$的表达式;
- 代入已知条件:将$x=1$时的$h'(1)=1$和$g'(1)=2$代入导数表达式;
- 解方程求$g(1)$:通过指数方程转化为对数方程,最终求出$g(1)$的值。
关键点:正确应用链式法则,准确处理指数与对数的转换关系。
-
求导过程
根据链式法则,函数$h(x)=e^{1+g(x)}$的导数为:
$h'(x) = e^{1+g(x)} \cdot g'(x)$
其中,外函数导数为$e^{u}$($u=1+g(x)$),内函数导数为$g'(x)$。 -
代入已知条件
当$x=1$时,已知$h'(1)=1$和$g'(1)=2$,代入导数表达式:
$1 = e^{1+g(1)} \cdot 2$ -
解方程求$g(1)$
- 两边同时除以2:
$e^{1+g(1)} = \frac{1}{2}$ - 取自然对数:
$1 + g(1) = \ln\left(\frac{1}{2}\right) = -\ln 2$ - 移项得:
$g(1) = -\ln 2 - 1$
- 两边同时除以2: