题目
1. lim _(xarrow 0)cot x(dfrac (1)(sin x)-dfrac (1)(x))= __
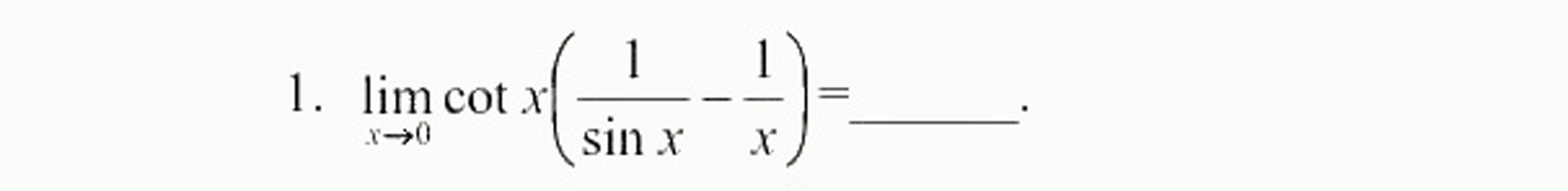
题目解答
答案
首先将极限里的函数通分,再用极限运算法则和等价无穷小的替换,就可以简单的求出极限。
$\lim _{x\rightarrow 0}\cot x(\dfrac {1}{\sin x}-\dfrac {1}{x})=\lim _{x\rightarrow 0}\dfrac {\cos x(x-\sin x)}{x\sin ^2x}$
$=\lim _{x\rightarrow 0}\dfrac {x-\sin x}{x^3}=\lim _{x\rightarrow 0}\dfrac {1-\cos x}{3x^2}$
$=\lim _{x\rightarrow 0}\dfrac {\frac {1}{2}x^2}{3x^2}=\dfrac {1}{6}$
$\lim _{x\rightarrow 0}\cot x(\dfrac {1}{\sin x}-\dfrac {1}{x})=\lim _{x\rightarrow 0}\dfrac {\cos x(x-\sin x)}{x\sin ^2x}$
$=\lim _{x\rightarrow 0}\dfrac {x-\sin x}{x^3}=\lim _{x\rightarrow 0}\dfrac {1-\cos x}{3x^2}$
$=\lim _{x\rightarrow 0}\dfrac {\frac {1}{2}x^2}{3x^2}=\dfrac {1}{6}$
解析
步骤 1:通分
将极限中的函数通分,得到 $\cot x(\dfrac {1}{\sin x}-\dfrac {1}{x})=\dfrac {\cos x(x-\sin x)}{x\sin ^2x}$。
步骤 2:使用极限运算法则
将通分后的表达式代入极限,得到 $\lim _{x\rightarrow 0}\dfrac {\cos x(x-\sin x)}{x\sin ^2x}$。
步骤 3:使用等价无穷小替换
将 $\sin x$ 替换为 $x$,得到 $\lim _{x\rightarrow 0}\dfrac {x-\sin x}{x^3}$。
步骤 4:使用洛必达法则
对分子和分母分别求导,得到 $\lim _{x\rightarrow 0}\dfrac {1-\cos x}{3x^2}$。
步骤 5:再次使用洛必达法则
对分子和分母再次求导,得到 $\lim _{x\rightarrow 0}\dfrac {\frac {1}{2}x^2}{3x^2}$。
步骤 6:计算极限
计算得到 $\lim _{x\rightarrow 0}\dfrac {\frac {1}{2}x^2}{3x^2}=\dfrac {1}{6}$。
将极限中的函数通分,得到 $\cot x(\dfrac {1}{\sin x}-\dfrac {1}{x})=\dfrac {\cos x(x-\sin x)}{x\sin ^2x}$。
步骤 2:使用极限运算法则
将通分后的表达式代入极限,得到 $\lim _{x\rightarrow 0}\dfrac {\cos x(x-\sin x)}{x\sin ^2x}$。
步骤 3:使用等价无穷小替换
将 $\sin x$ 替换为 $x$,得到 $\lim _{x\rightarrow 0}\dfrac {x-\sin x}{x^3}$。
步骤 4:使用洛必达法则
对分子和分母分别求导,得到 $\lim _{x\rightarrow 0}\dfrac {1-\cos x}{3x^2}$。
步骤 5:再次使用洛必达法则
对分子和分母再次求导,得到 $\lim _{x\rightarrow 0}\dfrac {\frac {1}{2}x^2}{3x^2}$。
步骤 6:计算极限
计算得到 $\lim _{x\rightarrow 0}\dfrac {\frac {1}{2}x^2}{3x^2}=\dfrac {1}{6}$。