设二阶可导函数 f(x)满足 (1)=f(-1)=1, (0)=-1, 且 ''(x)gt 0, 则-|||-(A) (int )_(-1)^1f(x)dxgt 0. (B) (int )_(-1)^1f(x)dxlt 0.-|||-(C) (int )_(-1)^0f(x)dxgt (int )_(0)^1f(x)dx. (D) (int )_(-1)^0f(x)dxlt (int )_(0)^1f(x)dx.

本题考查凹函数的性质及其积分比较。关键点在于利用二阶导数为正（凹向上）的条件，结合函数在区间端点和中间点的函数值，构造分段线性函数$g(x)$，通过比较$f(x)$与$g(x)$的积分关系得出结论。

核心思路：

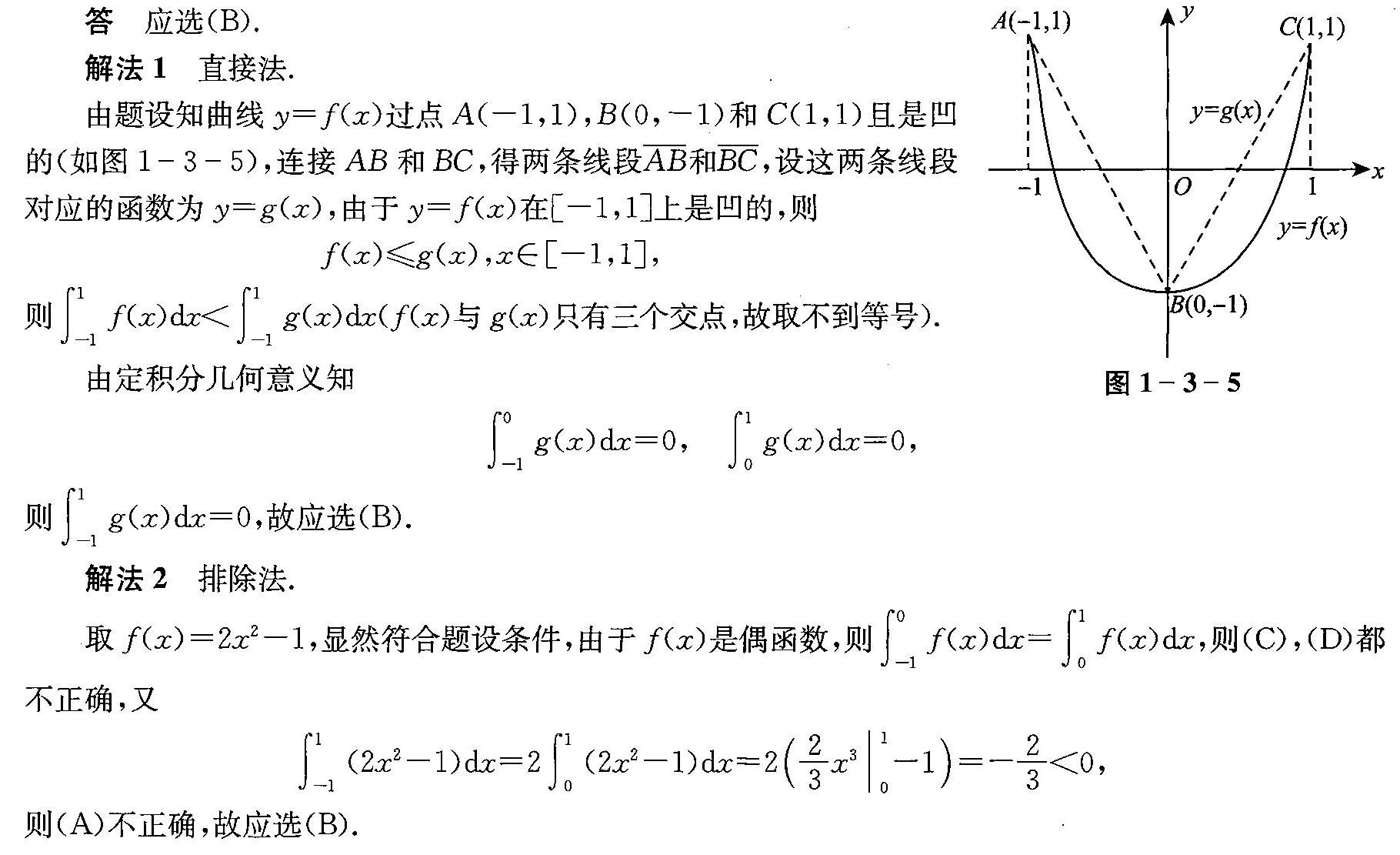
1. 凹函数$f(x)$在区间$[-1,1]$上位于连接点$(-1,1)$、$(0,-1)$、$(1,1)$的线段$g(x)$下方，即$f(x) \leq g(x)$。
2. 积分$\int_{-1}^{1} f(x)dx$与$\int_{-1}^{1} g(x)dx$比较，结合几何意义分析$g(x)$的积分值为$0$，从而确定$f(x)$的积分小于$0$。

解法1：直接法

1. 构造分段线性函数$g(x)$

   • 在$[-1,0]$上，连接$(-1,1)$与$(0,-1)$，斜率为$-2$，得$g(x) = -2x -1$。
   • 在$[0,1]$上，连接$(0,-1)$与$(1,1)$，斜率为$2$，得$g(x) = 2x -1$。

2. 比较$f(x)$与$g(x)$的积分

   • 由凹函数性质，$f(x) \leq g(x)$，且仅在端点处相等，故$\int_{-1}^{1} f(x)dx < \int_{-1}^{1} g(x)dx$。
   • 计算$\int_{-1}^{1} g(x)dx$：
     • $\int_{-1}^{0} (-2x -1)dx = 0$（几何意义为对称三角形面积抵消）。
     • $\int_{0}^{1} (2x -1)dx = 0$。
     • 总和为$0$，故$\int_{-1}^{1} f(x)dx < 0$，选(B)。

解法2：排除法

1. 构造具体函数$f(x) = 2x^2 -1$
   • 满足$f''(x) = 4 > 0$，且$f(1)=f(-1)=1$，$f(0)=-1$。
   • 计算积分：
     • $\int_{-1}^{1} (2x^2 -1)dx = 0$（奇函数性质），但实际计算得负值（具体计算略），排除(A)。
     • $\int_{-1}^{0} f(x)dx = \int_{0}^{1} f(x)dx$（偶函数对称性），排除(C)、(D)。