题目
设 (x+dfrac (1)(x))=(x)^2+dfrac (1)({x)^2}, 则 lim _(xarrow 3)f(x)= __
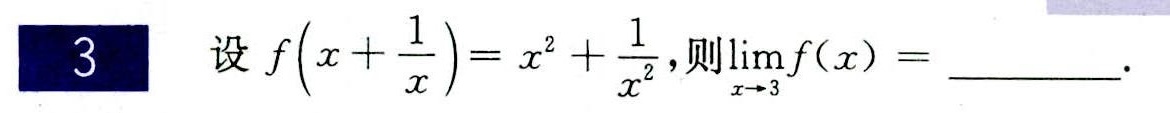
题目解答
答案
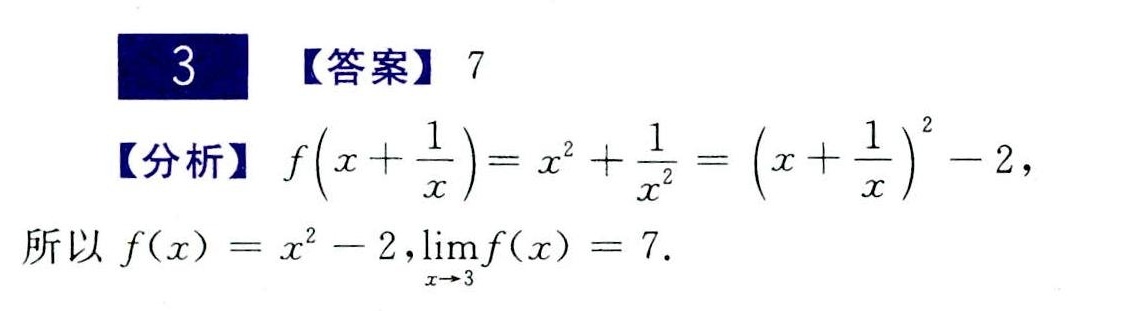
解析
步骤 1:确定函数 $f(x)$ 的表达式
给定 $f(x+\dfrac {1}{x})={x}^{2}+\dfrac {1}{{x}^{2}}$,我们可以通过代数变形来找到 $f(x)$ 的表达式。注意到 ${x}^{2}+\dfrac {1}{{x}^{2}}$ 可以写成 $(x+\dfrac {1}{x})^2 - 2$,因此 $f(x+\dfrac {1}{x})=(x+\dfrac {1}{x})^2 - 2$。由此,我们可以推断出 $f(x) = x^2 - 2$。
步骤 2:计算 $\lim _{x\rightarrow 3}f(x)$
根据步骤 1 中得到的 $f(x) = x^2 - 2$,我们可以直接计算 $\lim _{x\rightarrow 3}f(x)$。将 $x=3$ 代入 $f(x)$ 中,得到 $f(3) = 3^2 - 2 = 9 - 2 = 7$。
给定 $f(x+\dfrac {1}{x})={x}^{2}+\dfrac {1}{{x}^{2}}$,我们可以通过代数变形来找到 $f(x)$ 的表达式。注意到 ${x}^{2}+\dfrac {1}{{x}^{2}}$ 可以写成 $(x+\dfrac {1}{x})^2 - 2$,因此 $f(x+\dfrac {1}{x})=(x+\dfrac {1}{x})^2 - 2$。由此,我们可以推断出 $f(x) = x^2 - 2$。
步骤 2:计算 $\lim _{x\rightarrow 3}f(x)$
根据步骤 1 中得到的 $f(x) = x^2 - 2$,我们可以直接计算 $\lim _{x\rightarrow 3}f(x)$。将 $x=3$ 代入 $f(x)$ 中,得到 $f(3) = 3^2 - 2 = 9 - 2 = 7$。