题目
求曲线y=x^2,直线y=2x-1及x轴所围成的图形面积。
求曲线$$y=x^2$$,直线$$y=2x-1$$及$$x$$轴所围成的图形面积。
题目解答
答案
根据题意,绘图如下:
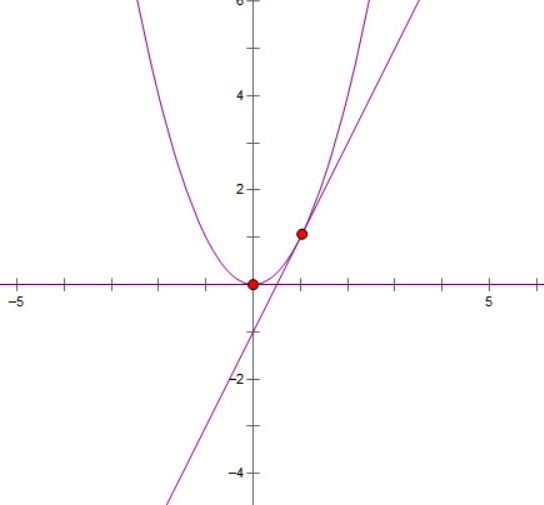
根据绘图可知:
直线$$y=2x-1$$与$$x$$轴的交点为$$(\frac{1}{2} ,0)$$
联立$$\cases { y=2x-1\cr y=x^2\cr}$$, 得到直线与曲线交点为$$(1,1)$$
所以可知,曲线$$y=x^2$$,直线$$y=2x-1$$及$$x$$轴所围成的图形面积为:
$$S=$$$$\int_{0}^{1} {x^2}\,{\rm dx}-\int_{\frac{1}{2} }^{1} {(2x-1) }\,{\rm dx}$$$$=\frac{1}{3} x^3|^1_0-(x^2-x)|^1_{\frac{1}{2} }$$$$=\frac{1}{3} -\frac{1}{4}$$$$=\frac{1}{12}$$
综上所述,所求面积为$$\frac{1}{12}$$
解析
步骤 1:确定交点
首先,我们需要确定曲线$$y=x^2$$与直线$$y=2x-1$$的交点。为此,我们联立这两个方程:
$$\cases { y=2x-1\cr y=x^2\cr}$$
解这个方程组,得到:
$$x^2=2x-1$$
$$x^2-2x+1=0$$
$$(x-1)^2=0$$
$$x=1$$
因此,交点为$$(1,1)$$。
步骤 2:确定与$$x$$轴的交点
接下来,我们需要确定直线$$y=2x-1$$与$$x$$轴的交点。为此,我们令$$y=0$$:
$$2x-1=0$$
$$x=\frac{1}{2}$$
因此,交点为$$(\frac{1}{2} ,0)$$。
步骤 3:计算面积
现在,我们已经确定了曲线$$y=x^2$$,直线$$y=2x-1$$及$$x$$轴所围成的图形的边界。接下来,我们计算这个图形的面积。根据图形的形状,我们可以将面积分为两部分:曲线$$y=x^2$$与$$x$$轴之间的面积,以及直线$$y=2x-1$$与$$x$$轴之间的面积。因此,面积$$S$$为:
$$S=$$$$\int_{0}^{1} {x^2}\,{\rm dx}-\int_{\frac{1}{2} }^{1} {(2x-1) }\,{\rm dx}$$
$$=\frac{1}{3} x^3|^1_0-(x^2-x)|^1_{\frac{1}{2} }$$
$$=\frac{1}{3} -\frac{1}{4}$$
$$=\frac{1}{12}$$
首先,我们需要确定曲线$$y=x^2$$与直线$$y=2x-1$$的交点。为此,我们联立这两个方程:
$$\cases { y=2x-1\cr y=x^2\cr}$$
解这个方程组,得到:
$$x^2=2x-1$$
$$x^2-2x+1=0$$
$$(x-1)^2=0$$
$$x=1$$
因此,交点为$$(1,1)$$。
步骤 2:确定与$$x$$轴的交点
接下来,我们需要确定直线$$y=2x-1$$与$$x$$轴的交点。为此,我们令$$y=0$$:
$$2x-1=0$$
$$x=\frac{1}{2}$$
因此,交点为$$(\frac{1}{2} ,0)$$。
步骤 3:计算面积
现在,我们已经确定了曲线$$y=x^2$$,直线$$y=2x-1$$及$$x$$轴所围成的图形的边界。接下来,我们计算这个图形的面积。根据图形的形状,我们可以将面积分为两部分:曲线$$y=x^2$$与$$x$$轴之间的面积,以及直线$$y=2x-1$$与$$x$$轴之间的面积。因此,面积$$S$$为:
$$S=$$$$\int_{0}^{1} {x^2}\,{\rm dx}-\int_{\frac{1}{2} }^{1} {(2x-1) }\,{\rm dx}$$
$$=\frac{1}{3} x^3|^1_0-(x^2-x)|^1_{\frac{1}{2} }$$
$$=\frac{1}{3} -\frac{1}{4}$$
$$=\frac{1}{12}$$