题目
求指导本题解题过程,谢谢您!4.设随机变量X的概率密度函数为 _(x)(x)= { , 0leqslant xleqslant 2, 0, . Y=2X+1 的概率密度-|||-函数.
求指导本题解题过程,谢谢您!
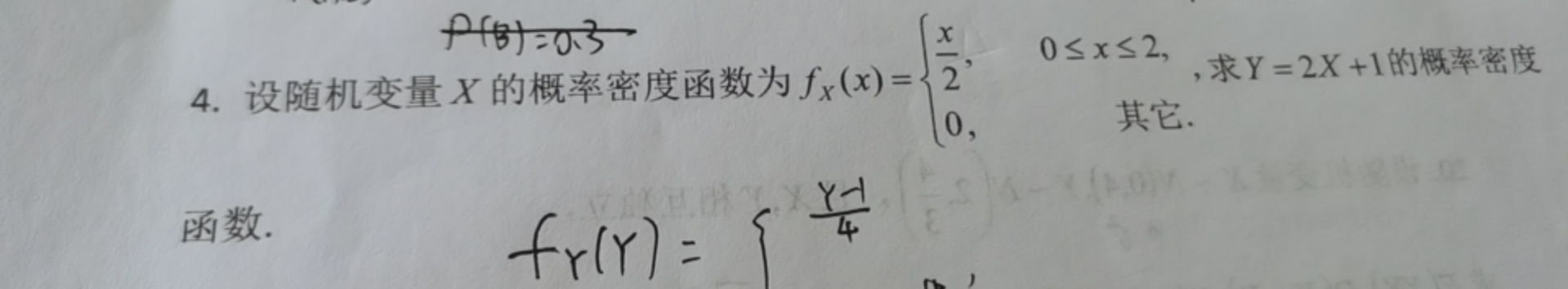
题目解答
答案

解析
步骤 1:确定Y的取值范围
由于 $Y = 2X + 1$,且 $X$ 的取值范围是 $0 \leqslant x \leqslant 2$,因此 $Y$ 的取值范围是 $1 \leqslant y \leqslant 5$。
步骤 2:求解Y的概率密度函数
根据概率密度函数的定义,$Y$ 的概率密度函数 $f_Y(y)$ 可以通过 $X$ 的概率密度函数 $f_X(x)$ 和 $Y$ 与 $X$ 的关系式 $Y = 2X + 1$ 来求解。首先,求解 $X$ 关于 $Y$ 的反函数,即 $X = \frac{Y - 1}{2}$。然后,根据概率密度函数的变换公式,$f_Y(y) = f_X(x) \cdot | \frac{dx}{dy} |$,其中 $| \frac{dx}{dy} |$ 是 $X$ 关于 $Y$ 的导数的绝对值。
步骤 3:计算导数并代入
$X = \frac{Y - 1}{2}$,则 $\frac{dx}{dy} = \frac{1}{2}$,因此 $| \frac{dx}{dy} | = \frac{1}{2}$。将 $X = \frac{Y - 1}{2}$ 代入 $f_X(x)$,得到 $f_X(\frac{Y - 1}{2}) = \frac{1}{2} \cdot \frac{Y - 1}{2} = \frac{Y - 1}{4}$。因此,$f_Y(y) = \frac{Y - 1}{4} \cdot \frac{1}{2} = \frac{Y - 1}{8}$。
步骤 4:确定Y的概率密度函数
根据步骤 1 和步骤 3 的结果,$Y$ 的概率密度函数为 $f_Y(y) = \frac{Y - 1}{8}$,其中 $1 \leqslant y \leqslant 5$。
由于 $Y = 2X + 1$,且 $X$ 的取值范围是 $0 \leqslant x \leqslant 2$,因此 $Y$ 的取值范围是 $1 \leqslant y \leqslant 5$。
步骤 2:求解Y的概率密度函数
根据概率密度函数的定义,$Y$ 的概率密度函数 $f_Y(y)$ 可以通过 $X$ 的概率密度函数 $f_X(x)$ 和 $Y$ 与 $X$ 的关系式 $Y = 2X + 1$ 来求解。首先,求解 $X$ 关于 $Y$ 的反函数,即 $X = \frac{Y - 1}{2}$。然后,根据概率密度函数的变换公式,$f_Y(y) = f_X(x) \cdot | \frac{dx}{dy} |$,其中 $| \frac{dx}{dy} |$ 是 $X$ 关于 $Y$ 的导数的绝对值。
步骤 3:计算导数并代入
$X = \frac{Y - 1}{2}$,则 $\frac{dx}{dy} = \frac{1}{2}$,因此 $| \frac{dx}{dy} | = \frac{1}{2}$。将 $X = \frac{Y - 1}{2}$ 代入 $f_X(x)$,得到 $f_X(\frac{Y - 1}{2}) = \frac{1}{2} \cdot \frac{Y - 1}{2} = \frac{Y - 1}{4}$。因此,$f_Y(y) = \frac{Y - 1}{4} \cdot \frac{1}{2} = \frac{Y - 1}{8}$。
步骤 4:确定Y的概率密度函数
根据步骤 1 和步骤 3 的结果,$Y$ 的概率密度函数为 $f_Y(y) = \frac{Y - 1}{8}$,其中 $1 \leqslant y \leqslant 5$。