题目
已知随机变量的分布函数,求
已知随机变量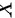 的分布函数
的分布函数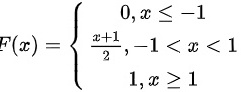 ,求
,求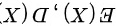
题目解答
答案
由题意得,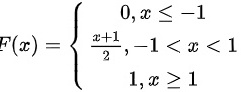 ,
,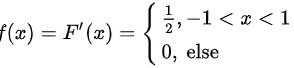 ,
,
,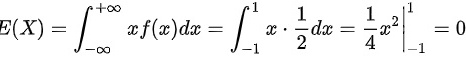 ,
,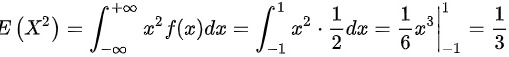 ,
,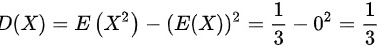 ,故
,故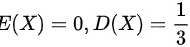
解析
步骤 1:求概率密度函数
由分布函数$f(x)$,求导得到概率密度函数$f(x)$。对于给定的分布函数$f(x)=$ $\left \{ \begin{matrix} 0,x\leqslant -1\\ \dfrac {x+1}{2},-1\lt x\lt 1\\ 1,x\geqslant 1\end{matrix} \right.$,其导数$f'(x)$即为概率密度函数$f(x)$。在区间$(-1,1)$内,$f'(x)=\dfrac{1}{2}$,其他区间$f(x)=0$。
步骤 2:求期望E(X)
期望$E(X)$的计算公式为$E(X)=\int_{-\infty}^{\infty}xf(x)dx$。根据概率密度函数$f(x)$,$E(X)=\int_{-1}^{1}x\cdot\dfrac{1}{2}dx$。计算得$E(X)=\dfrac{1}{2}\int_{-1}^{1}xdx=\dfrac{1}{2}\cdot\dfrac{1}{2}x^2|_{-1}^{1}=\dfrac{1}{2}\cdot\dfrac{1}{2}(1^2-(-1)^2)=0$。
步骤 3:求方差D(X)
方差$D(X)$的计算公式为$D(X)=E(X^2)-[E(X)]^2$。首先计算$E(X^2)=\int_{-\infty}^{\infty}x^2f(x)dx$。根据概率密度函数$f(x)$,$E(X^2)=\int_{-1}^{1}x^2\cdot\dfrac{1}{2}dx$。计算得$E(X^2)=\dfrac{1}{2}\int_{-1}^{1}x^2dx=\dfrac{1}{2}\cdot\dfrac{1}{3}x^3|_{-1}^{1}=\dfrac{1}{2}\cdot\dfrac{1}{3}(1^3-(-1)^3)=\dfrac{1}{3}$。因此,$D(X)=E(X^2)-[E(X)]^2=\dfrac{1}{3}-0^2=\dfrac{1}{3}$。
由分布函数$f(x)$,求导得到概率密度函数$f(x)$。对于给定的分布函数$f(x)=$ $\left \{ \begin{matrix} 0,x\leqslant -1\\ \dfrac {x+1}{2},-1\lt x\lt 1\\ 1,x\geqslant 1\end{matrix} \right.$,其导数$f'(x)$即为概率密度函数$f(x)$。在区间$(-1,1)$内,$f'(x)=\dfrac{1}{2}$,其他区间$f(x)=0$。
步骤 2:求期望E(X)
期望$E(X)$的计算公式为$E(X)=\int_{-\infty}^{\infty}xf(x)dx$。根据概率密度函数$f(x)$,$E(X)=\int_{-1}^{1}x\cdot\dfrac{1}{2}dx$。计算得$E(X)=\dfrac{1}{2}\int_{-1}^{1}xdx=\dfrac{1}{2}\cdot\dfrac{1}{2}x^2|_{-1}^{1}=\dfrac{1}{2}\cdot\dfrac{1}{2}(1^2-(-1)^2)=0$。
步骤 3:求方差D(X)
方差$D(X)$的计算公式为$D(X)=E(X^2)-[E(X)]^2$。首先计算$E(X^2)=\int_{-\infty}^{\infty}x^2f(x)dx$。根据概率密度函数$f(x)$,$E(X^2)=\int_{-1}^{1}x^2\cdot\dfrac{1}{2}dx$。计算得$E(X^2)=\dfrac{1}{2}\int_{-1}^{1}x^2dx=\dfrac{1}{2}\cdot\dfrac{1}{3}x^3|_{-1}^{1}=\dfrac{1}{2}\cdot\dfrac{1}{3}(1^3-(-1)^3)=\dfrac{1}{3}$。因此,$D(X)=E(X^2)-[E(X)]^2=\dfrac{1}{3}-0^2=\dfrac{1}{3}$。