题目
欲做一个底为正方形,客积 108 立方米的长方体开口容器 ,问该容器的底边和高各为多少米时用样最省?
欲做一个底为正方形,客积 108 立方米的长方体开口容器 ,问该容器的底边和高各为多少米时用样最省?
题目解答
答案
解:设容器底边的边长为 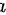 ,高为
,高为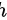 。
。
则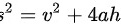
又∵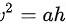 ,可以得到
,可以得到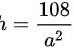
代入到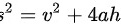 ,
,
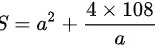
对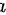 进行求导,则
进行求导,则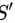
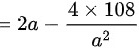
令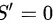 解得
解得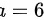
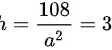
由此可以得出答案底面边长为6m,高3m是时用料最省
解析
步骤 1:定义变量
设容器底边的边长为 $x$ 米,高为 $h$ 米。
步骤 2:建立体积方程
根据题意,容器的体积为 $108$ 立方米,因此有 $x^2h = 108$。
步骤 3:建立表面积方程
容器的表面积 $S$ 包括底面和四个侧面,即 $S = x^2 + 4xh$。
步骤 4:用体积方程表示高
从体积方程 $x^2h = 108$ 可得 $h = \frac{108}{x^2}$。
步骤 5:将高代入表面积方程
将 $h = \frac{108}{x^2}$ 代入表面积方程 $S = x^2 + 4xh$,得到 $S = x^2 + 4x\left(\frac{108}{x^2}\right) = x^2 + \frac{432}{x}$。
步骤 6:求导数
对 $S$ 关于 $x$ 求导,得到 $S' = 2x - \frac{432}{x^2}$。
步骤 7:求导数为零的点
令 $S' = 0$,即 $2x - \frac{432}{x^2} = 0$,解得 $x^3 = 216$,从而 $x = 6$。
步骤 8:求高
将 $x = 6$ 代入 $h = \frac{108}{x^2}$,得到 $h = \frac{108}{6^2} = 3$。
步骤 9:验证
验证 $x = 6$ 时,$S$ 取得最小值,即 $S = 6^2 + \frac{432}{6} = 36 + 72 = 108$。
设容器底边的边长为 $x$ 米,高为 $h$ 米。
步骤 2:建立体积方程
根据题意,容器的体积为 $108$ 立方米,因此有 $x^2h = 108$。
步骤 3:建立表面积方程
容器的表面积 $S$ 包括底面和四个侧面,即 $S = x^2 + 4xh$。
步骤 4:用体积方程表示高
从体积方程 $x^2h = 108$ 可得 $h = \frac{108}{x^2}$。
步骤 5:将高代入表面积方程
将 $h = \frac{108}{x^2}$ 代入表面积方程 $S = x^2 + 4xh$,得到 $S = x^2 + 4x\left(\frac{108}{x^2}\right) = x^2 + \frac{432}{x}$。
步骤 6:求导数
对 $S$ 关于 $x$ 求导,得到 $S' = 2x - \frac{432}{x^2}$。
步骤 7:求导数为零的点
令 $S' = 0$,即 $2x - \frac{432}{x^2} = 0$,解得 $x^3 = 216$,从而 $x = 6$。
步骤 8:求高
将 $x = 6$ 代入 $h = \frac{108}{x^2}$,得到 $h = \frac{108}{6^2} = 3$。
步骤 9:验证
验证 $x = 6$ 时,$S$ 取得最小值,即 $S = 6^2 + \frac{432}{6} = 36 + 72 = 108$。