题目
设是抛物面, 取下侧, 则曲面积分( ) .
设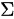 是抛物面
是抛物面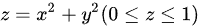 , 取下侧, 则曲面积分
, 取下侧, 则曲面积分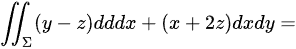 ( ) .
( ) .
题目解答
答案
首先,抛物面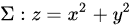 (其中
(其中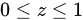 )在xOy平面上的投影区域D是一个单位圆,即
)在xOy平面上的投影区域D是一个单位圆,即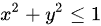 。
。
由于抛物面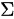 取下侧,我们可以使用投影法来计算曲面积分。具体来说,我们需要将曲面积分转化为在投影区域D上的二重积分,并乘以曲面在该点处的法向量的z分量(注意这里是下侧,所以法向量的z分量是负的)。
取下侧,我们可以使用投影法来计算曲面积分。具体来说,我们需要将曲面积分转化为在投影区域D上的二重积分,并乘以曲面在该点处的法向量的z分量(注意这里是下侧,所以法向量的z分量是负的)。
抛物面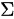 在点
在点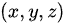 处的法向量为
处的法向量为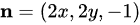 ,因为曲面方程是
,因为曲面方程是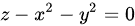 ,对x, y, z分别求偏导得到法向量的三个分量。注意这里法向量的z分量是-1,因为抛物面开口向上,下侧的法向量指向z轴的负方向。
,对x, y, z分别求偏导得到法向量的三个分量。注意这里法向量的z分量是-1,因为抛物面开口向上,下侧的法向量指向z轴的负方向。
但是,由于曲面积分中的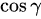 (即法向量与z轴正方向的夹角的余弦值)在这里是负的(因为法向量指向z轴负方向),所以在计算时我们可以直接取法向量的z分量的绝对值,即1,并注意到积分时应该取负号(因为曲面取下侧)。
(即法向量与z轴正方向的夹角的余弦值)在这里是负的(因为法向量指向z轴负方向),所以在计算时我们可以直接取法向量的z分量的绝对值,即1,并注意到积分时应该取负号(因为曲面取下侧)。
然而,在这个特定的问题中,由于被积函数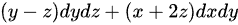 中,只有dxdy部分与法向量的z分量有关(通过
中,只有dxdy部分与法向量的z分量有关(通过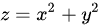 代入),并且
代入),并且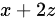 这一项在代入z后并不包含与曲面法向量直接相关的项(即不包含额外的dz或dy),因此实际上我们不需要显式地考虑法向量的z分量。但为了保持逻辑清晰,我们还是按照上面的思路来解释。
这一项在代入z后并不包含与曲面法向量直接相关的项(即不包含额外的dz或dy),因此实际上我们不需要显式地考虑法向量的z分量。但为了保持逻辑清晰,我们还是按照上面的思路来解释。
不过,在这个问题中,我们实际上只需要计算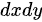 部分的积分,因为
部分的积分,因为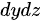 部分与题目给出的被积函数不匹配。
部分与题目给出的被积函数不匹配。
将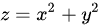 代入
代入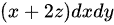 ,得到:
,得到:
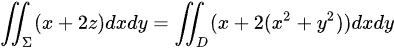 其中D是单位圆
其中D是单位圆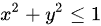 。
。
接下来,在极坐标系下计算这个二重积分:
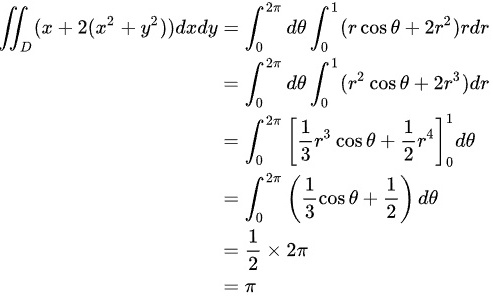
故答案为: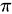 。
。