14.今有甲、乙两名射手轮流对同一目标进行射击,甲命中的概率为p1,乙命中的概率为p2.-|||-甲先射,谁先命中谁得胜,分别求甲、乙两人获胜的概率.

题目解答
答案
解:令A,B分别表示"甲获胜",乙获胜",$$A_{1}$$ $$B_{1}(i=1,2,\cdot \cdot \cdot )$$分别表示"甲第i次射击命中""乙第i次射击命中",则有 $$A=A_{1}$$$$\cup \overrightarrow {A_{1}B_{1}}A_{2} \cup \overrightarrow {B_{1}A_{2}B_{2}$$ $$B=\bar {A_{1}}B_{1}$$$$\cup \overrightarrow {A_{1}B_{1}A_{2}}B_{2}\cup \overrightarrow {A_{1}B_{1}A_{$$ 因而 $$P(A)=P(A_{1})+P( , )+P( BA_{1}B_{2})$$ $$=P(A_{1})+P(A_{1})P(B_{1})P(A_{2})+$$$$P(A_{1})P(B_{1})P(A_{2})P$$ $$+\cdot \cdot \cdot $$ $$=p_{1}+(1-p_{1})(1-p_{2})p_{1}+(1$$$$p_{1})^{2}$$ $$(1-p_{2})^{3}p_{1}+\cdot \cdot \cdot $$ $$=\frac{p_{1}}{1-(1-p_{1})(1-p_{2})}$$$$\frac{p_{1}}{p_{1}+p_{2}-p_{1}p_{2}}$$ ,因为A与B互为逆事件,所以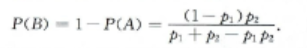
解析
考查要点:本题主要考查几何分布和无限等比数列求和的应用,以及如何将实际问题转化为概率模型。
解题核心思路:
- 分解事件:将甲、乙获胜的所有可能情况分解为无限次射击中的各个独立事件。
- 等比数列求和:利用等比数列求和公式,将无限次射击的概率总和转化为闭合表达式。
- 互斥事件关系:甲、乙获胜的概率之和为1,简化计算。
破题关键点:
- 甲获胜的条件:甲在第1次、第3次、第5次等奇数次射击中首次命中,且之前所有射击均未命中。
- 乙获胜的条件:乙在第2次、第4次、第6次等偶数次射击中首次命中,且之前所有射击均未命中。
- 独立事件性质:每次射击结果相互独立,概率可相乘。
甲获胜的概率推导
甲获胜的可能情况包括:
- 第1次命中:概率为 $p_1$。
- 第3次命中:前两次均未命中(甲第1次未命中且乙第1次未命中),概率为 $(1-p_1)(1-p_2)p_1$。
- 第5次命中:前四次均未命中,概率为 $(1-p_1)^2(1-p_2)^2p_1$。
以此类推,形成首项为 $p_1$,公比为 $(1-p_1)(1-p_2)$ 的等比数列。
总概率为:
$P(A) = p_1 + (1-p_1)(1-p_2)p_1 + [(1-p_1)(1-p_2)]^2p_1 + \cdots$
利用等比数列求和公式:
$P(A) = \frac{p_1}{1 - (1-p_1)(1-p_2)} = \frac{p_1}{p_1 + p_2 - p_1p_2}$
乙获胜的概率推导
乙获胜的可能情况包括:
- 第2次命中:甲第1次未命中且乙第1次命中,概率为 $(1-p_1)p_2$。
- 第4次命中:前四次均未命中,概率为 $(1-p_1)^2(1-p_2)^1p_2$。
以此类推,形成首项为 $(1-p_1)p_2$,公比为 $(1-p_1)(1-p_2)$ 的等比数列。
总概率为:
$P(B) = (1-p_1)p_2 + (1-p_1)^2(1-p_2)p_2 + \cdots$
利用等比数列求和公式:
$P(B) = \frac{(1-p_1)p_2}{1 - (1-p_1)(1-p_2)} = \frac{(1-p_1)p_2}{p_1 + p_2 - p_1p_2}$