题目
(1)设 dfrac (cos x)(x) 是f(x)的一个原函数,则 int xf'(x)dx= __ ;

题目解答
答案
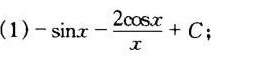
解析
步骤 1:确定原函数
已知 $\dfrac {\cos x}{x}$ 是f(x)的一个原函数,即 $\int f(x)dx = \dfrac {\cos x}{x} + C$。
步骤 2:求导
对 $\dfrac {\cos x}{x}$ 求导,得到 $f(x)$。
$f(x) = \dfrac {d}{dx} \left( \dfrac {\cos x}{x} \right) = \dfrac {-x\sin x - \cos x}{x^2}$
步骤 3:计算 $\int xf'(x)dx$
根据分部积分法,$\int xf'(x)dx = xf(x) - \int f(x)dx$。
代入 $f(x)$ 和 $\int f(x)dx$ 的表达式,得到:
$\int xf'(x)dx = x \cdot \dfrac {-x\sin x - \cos x}{x^2} - \dfrac {\cos x}{x} + C$
化简得到:
$\int xf'(x)dx = -\sin x - \dfrac {2\cos x}{x} + C$
已知 $\dfrac {\cos x}{x}$ 是f(x)的一个原函数,即 $\int f(x)dx = \dfrac {\cos x}{x} + C$。
步骤 2:求导
对 $\dfrac {\cos x}{x}$ 求导,得到 $f(x)$。
$f(x) = \dfrac {d}{dx} \left( \dfrac {\cos x}{x} \right) = \dfrac {-x\sin x - \cos x}{x^2}$
步骤 3:计算 $\int xf'(x)dx$
根据分部积分法,$\int xf'(x)dx = xf(x) - \int f(x)dx$。
代入 $f(x)$ 和 $\int f(x)dx$ 的表达式,得到:
$\int xf'(x)dx = x \cdot \dfrac {-x\sin x - \cos x}{x^2} - \dfrac {\cos x}{x} + C$
化简得到:
$\int xf'(x)dx = -\sin x - \dfrac {2\cos x}{x} + C$