题目
9.设某电子管的使用寿命X(单位为小时)服从参数为 lambda =0.0002 的指数分布,求电子管-|||-的使用寿命超过3000小时的概率.

题目解答
答案
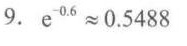
解析
步骤 1:确定指数分布的概率密度函数
指数分布的概率密度函数为 $f(x) = \lambda e^{-\lambda x}$,其中 $\lambda$ 是分布的参数,$x$ 是随机变量的取值。在这个问题中,$\lambda = 0.0002$。
步骤 2:计算电子管使用寿命超过3000小时的概率
电子管的使用寿命超过3000小时的概率可以通过计算 $P(X > 3000)$ 来得到。根据指数分布的性质,$P(X > x) = e^{-\lambda x}$。将 $\lambda = 0.0002$ 和 $x = 3000$ 代入,得到 $P(X > 3000) = e^{-0.0002 \times 3000}$。
步骤 3:计算最终结果
计算 $e^{-0.0002 \times 3000}$ 的值,得到 $e^{-0.6}$。使用计算器或查表得到 $e^{-0.6} \approx 0.5488$。
指数分布的概率密度函数为 $f(x) = \lambda e^{-\lambda x}$,其中 $\lambda$ 是分布的参数,$x$ 是随机变量的取值。在这个问题中,$\lambda = 0.0002$。
步骤 2:计算电子管使用寿命超过3000小时的概率
电子管的使用寿命超过3000小时的概率可以通过计算 $P(X > 3000)$ 来得到。根据指数分布的性质,$P(X > x) = e^{-\lambda x}$。将 $\lambda = 0.0002$ 和 $x = 3000$ 代入,得到 $P(X > 3000) = e^{-0.0002 \times 3000}$。
步骤 3:计算最终结果
计算 $e^{-0.0002 \times 3000}$ 的值,得到 $e^{-0.6}$。使用计算器或查表得到 $e^{-0.6} \approx 0.5488$。