题目
设l为椭圆dfrac ({x)^2}(4)+dfrac ({y)^2}(3)=1,其周长记为a,则dfrac ({x)^2}(4)+dfrac ({y)^2}(3)=1=______.
设l为椭圆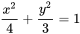 ,其周长记为a,则
,其周长记为a,则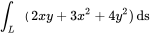 =______.
=______.
题目解答
答案

解析
考查要点:本题主要考查曲线积分的对称性应用以及椭圆方程的代数变形。关键在于利用椭圆的对称性简化积分计算。
解题思路:
- 代数变形:将椭圆方程转化为标准形式,找到与被积函数相关的代数关系,简化积分表达式。
- 对称性分析:利用椭圆关于坐标轴的对称性,判断被积函数的奇偶性,从而快速确定某些积分项的值。
- 几何意义:将剩余的常数项积分转化为椭圆周长的倍数。
步骤1:椭圆方程变形
椭圆方程为 $\dfrac{x^2}{4} + \dfrac{y^2}{3} = 1$,两边同乘12得:
$3x^2 + 4y^2 = 12$
步骤2:简化被积函数
将原积分表达式 $(2xy + 3x^2 + 4y^2) \, ds$ 中的 $3x^2 + 4y^2$ 替换为12:
$2xy + 3x^2 + 4y^2 = 2xy + 12$
步骤3:拆分积分项
原积分拆分为两部分:
$\int_L (2xy + 12) \, ds = \int_L 2xy \, ds + \int_L 12 \, ds$
步骤4:利用对称性计算 $\int_L 2xy \, ds$
椭圆关于x轴对称,而被积函数 $xy$ 是关于y的奇函数(将$y$替换为$-y$后符号改变)。因此:
$\int_L xy \, ds = 0 \quad \Rightarrow \quad \int_L 2xy \, ds = 0$
步骤5:计算 $\int_L 12 \, ds$
$\int_L 12 \, ds$ 表示常数12乘以椭圆周长,即:
$\int_L 12 \, ds = 12a$
最终结果
将两部分结果相加:
$\int_L (2xy + 3x^2 + 4y^2) \, ds = 0 + 12a = 12a$